To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ohmic contactAn ohmic contact is a region on a semiconductor device that has been prepared so that the current-voltage (I-V) curve of the device is linear and symmetric. If the I-V characteristic is non-linear and asymmetric, the contact can instead be termed a blocking or Schottky contact. Typical ohmic contacts on semiconductors are sputtered or evaporated metal pads that are patterned using photolithography. Low-resistance, stable contacts are critical for the performance and reliability of integrated circuits and their preparation and characterization are major efforts in circuit fabrication. Product highlight
TheoryThe Fermi level (or strictly speaking, chemical potential) of any two solids in contact must be equal in thermal equilibrium. The difference between the Fermi energy and the vacuum level is termed the work function. A contact metal and a semiconductor can have different work functions, φM and φS respectively. If so, when the two materials are placed in contact, electrons will flow from the one with the lower work function until the Fermi levels equilibrate. As a result, the material with the lower work function will take on a slight positive charge while that with the higher work function will become slightly negative. The resulting electrostatic potential is termed the built-in field designated by Vbi. This contact potential will occur between any two solids and is the underlying cause of phenomena such as rectification in diodes and the Seebeck effect. The built-in field is the cause of band-bending in the semiconductor near the junction. Noticeable band-bending does not occur in metals since their very short screening length means that any electrical field extends only a short distance beyond the interface.
In a classical physics picture, in order to surmount the barrier, a carrier in the semiconductor must gain enough energy to jump from the Fermi level to the top of the bent conduction band. The needed barrier-surmounting energy φB is the sum of the built-in potential and the offset between the Fermi level and the conduction band. Equivalently for n-type semiconductors, φB = φM − χS where χS is the semiconductor's electron affinity, defined to be the difference between the vacuum level and the conduction band (CB) level. For p-type materials, φB = Eg − (φM − χS) where Eg is the bandgap. When the excitation over the barrier is thermal, the process is called thermionic emission. An equally important process in real contacts is quantum mechanical tunneling. The WKB approximation describes the simplest picture of tunnelling in which the probability of barrier penetration is exponentially dependent on the product of the barrier height and thickness. In the case of contacts, the thickness is given by the depletion width, which is the length scale that the built-in field penetrates into the semiconductor. The width of the depletion layer W can be calculated by solving Poisson's equation and considering the presence of dopants in the semiconductor: where in MKS units ρ is the net charge density and ε is the dielectric constant. The geometry is one-dimensional since the interface is assumed to be planar. Integrating the equation once, we get The constant of integration where the fact that V(0) = Vbi has been used to fix the remaining integration constant. This equation for V(x) describes the dashed blue curves in the right-hand panels of the figures. The depletion width can then be determined by setting V(W) = 0 which results in For 0 < x < W, ρ = eNdopant is the net charge density of ionized donor or acceptors Ndopant in the completely depleted semiconductor and e is the electronic charge. ρ and Vbi have positive signs for n-type semiconductors and negative signs for p-type semiconductors giving the positive curvature V''(x) for n-type and negative curvature for p-type as shown in the figures. Note from this crude derivation that the barrier height (dependent on electron affinity and built-in field) and barrier thickness (dependent on built-in field, semiconductor dielectric constant and doping density) can only be modified by changing the metal or changing the doping density. In general an engineer will choose a contact metal to be conductive, non-reactive, thermally stable, electrically stable and low-stress, and then will increase the doping density below the contact to narrow the width of the barrier region. The highly doped regions are termed n + or p + depending on the carrier type. Since the transmission coefficient in tunneling depends exponentially on particle mass, semiconductors with lower effective masses are more easily contacted. In addition, semiconductors with smaller bandgaps more readily form ohmic contacts because their electron affinities (and thus barrier heights) tend to be lower. The simple theory presented above predicts that φB = φM − χS, so naively metals whose work functions are close to the semiconductor's electron affinity should most easily form ohmic contacts. In fact, metals with high work functions form the best contacts to p-type semiconductors while those with low work functions form the best contacts to n-type semiconductors. Unfortunately experiments have shown that the predictive power of the model doesn't extend much beyond this statement. Under realistic conditions, contact metals may react with semiconductor surfaces to form a compound with new electronic properties. A contamination layer at the interface may effectively widen the barrier. The surface of the semiconductor may reconstruct leading to a new electronic state. The dependence of contact resistance on the details of the interfacial chemistry is what makes the reproducible fabrication of ohmic contacts such a manufacturing challenge. Preparation and characterization of ohmic contactsThe fabrication of ohmic contacts is a much-studied part of materials engineering that nonetheless remains something of an art. The reproducible, reliable fabrication of contacts relies on extreme cleanliness of the semiconductor surface. Since a native oxide rapidly forms on the surface of silicon, for example, the performance of a contact can depend sensitively on the details of preparation. The fundamental steps in contact fabrication are semiconductor surface cleaning, contact metal deposition, patterning and annealing. Surface cleaning may be performed by sputter-etching, chemical etching, reactive gas etching or ion milling. For example, the native oxide of silicon may be removed with an HF dip, while GaAs is more typically cleaned by a bromine-methanol dip. After cleaning metals are deposited via sputter deposition, evaporation or chemical vapor deposition (CVD). Sputtering is a faster and more convenient method of metal deposition than evaporation but the ion bombardment from the plasma may induce surface states or even invert the charge carrier type at the surface. For this reason the gentler but still rapid CVD is increasingly preferred. Patterning of contacts is accomplished with standard photolithographic methods such as lift-off, where contact metal is deposited through holes in a photoresist layer that is later dissolved away. Post-deposition annealing of contacts is useful for relieving stress as well as for inducing any desirable reactions between the metal and the semiconductor. The measurement of contact resistance is most simply performed using a four-point probe although for more accurate determination, use of the transmission line method is typical. Technologically important kinds of contactsModern ohmic contacts to silicon such as titanium-tungsten disilicide are usually silicides made by CVD. Contacts are often made by depositing the transition metal and forming the silicide by annealing with the result that the silicide may be non-stoichiometric. Silicide contacts can also be deposited by direct sputtering of the compound or by ion implantation of the transition metal followed by annealing. Aluminum is another important contact metal for silicon which can be used with either the n-type or p-type semiconductor. As with other reactive metals, Al contributes to contact formation by consuming the oxygen in the native oxide. Silicides have largely replaced Al in part because the more refractory materials are less prone to diffuse into unintended areas especially during subsequent high-temperature processing. Formation of contacts to compound semiconductors is considerably more difficult than with silicon. For example, GaAs surfaces tend to lose arsenic and the trend towards As loss can be considerably exacerbated by the deposition of metal. In addition, the volatility of As limits the amount of post-deposition annealing that GaAs devices will tolerate. One solution for GaAs and other compound semiconductors is to deposit a low-bandgap alloy contact layer as opposed to a heavily doped layer. For example, GaAs itself has a smaller bandgap than AlGaAs and so a layer of GaAs near its surface can promote ohmic behavior. In general the technology of ohmic contacts for III-V and II-VI semiconductors is much less developed than for Si.
Transparent or semi-transparent contacts are necessary for active matrix LCD displays, optoelectronic devices such as laser diodes and photovoltaics. The most popular choice is indium tin oxide, a metal that is formed by reactive sputtering of an In-Sn target in an oxide atmosphere. SignificanceThe RC time constant associated with contact resistance can limit the frequency response of devices. The charging and discharging of the leads resistance is a major cause of power dissipation in high clock rate digital electronics. Contact resistance causes power dissipation via Joule heating in low frequency and analog circuits (for example, solar cells) made from less common semiconductors. The establishment of a contact fabrication methodology is a critical part of the technological development of any new semiconductor. Electromigration and delamination at contacts are also a limitation on the lifetime of electronic devices. References
See also
Categories: Materials science | Condensed matter physics |
|||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ohmic_contact". A list of authors is available in Wikipedia. |




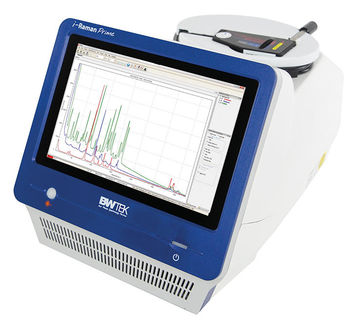

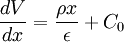
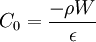 due to the definition of the depletion width as the length over which the interface is fully screened. Then
due to the definition of the depletion width as the length over which the interface is fully screened. Then