To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Opacity (optics)
Opacity is the state of being impenetrable to light. An opaque object is neither transparent (allowing all light to pass through) nor translucent (allowing some light to pass through). When light strikes an interface between two substances, some of the light is reflected, some is absorbed, and the rest is transmitted (see also refraction). An opaque substance transmits very little light, and therefore reflects or absorbs most of it. Both mirrors and jet are opaque. Opacity depends on the frequency of the light being considered. For instance, some kinds of glass, while completely transparent in the visual range, are largely opaque to ultraviolet light. More extreme frequency-dependence is visible in the absorption lines of cold gases. In general, a material tends to emit light in the same proportions as it absorbs it; this is the reason for the equivalence of absorption and emission lines. Product highlight
Numerical definitionWhile many materials are so opaque (steel in visible light having near-infinite opacity), and others so transparent (air in visible light having near-zero opacity), that opacity often seems to be a boolean property, others are "somewhat" opaque. Opacity is then in general a static variable: κν, where the ν indicates the continuum in question. It has units of reverse length, and is also called the absorption coefficient (see also the opposite extinction coefficient). It gives the proportional rate of absorption (or extinction or how much light intensity is lost for each metre) along a ray of light: In astronomy and planetary imaging fields, Tau defines the opacity: zero indicates wholly solid and higher numbers indicate more and more opaque in an inverse exponential fashion, for example a Tau of 1 indicates 36 percent of the light passes (e-1 = 0.36), and a Tau of 5 indicates less than 1 percent passes (e -5 = 0.0067).[citation needed][1] In astrophysics and plasma physics a term "opacity" often refers to an average of the above, calculated using a certain weighting scheme. Planck opacity uses normalized Planck black body radiation energy density distribution as the weighting function, and averages κν directly. Rosseland opacity, on the other hand, uses a temperature derivative of Planck distribution (normalized) as the weighting function, and averages 1 / κν, which is a photon mean free path; the average mean free path is then inverted to obtain opacity. ApplicationsIn astrophysics, the variations in opacity within a star are important to the understanding of radiation transfer in stellar atmospheres and the spectra we observe. In several types of chemical analysis, the concentration of a sample in a transparent medium (typically air or water) is determined via measuring its opacity or absorbance. In spectrophotometry the device identifies the sample's constituent substances from their absorbances. Opacity is also used as a measurement of particulate emissions. Extinction coefficientThe extinction coefficient for a particular substance is a measure of how well it scatters and absorbs electromagnetic radiation (EM waves). If the EM wave can pass through very easily, the material has a low extinction coefficient. Conversely, if the radiation hardly penetrates the material, but rather quickly becomes "extinct" within it, the extinction coefficient is high. A material can behave differently for different wavelengths of electromagnetic radiation. Glass is transparent to visible light, but many types of glass are opaque to ultra-violet wavelengths. In general, the extinction coefficient for any material is a function of the incident wavelength. The extinction coefficient is used widely in ultraviolet-visible spectroscopy. Physical definitionsThe parameter used to describe the interaction of electromagnetic radiation with matter is the complex index of refraction, ñ, which is a combination of a real part and an imaginary part: Here, n is also called the index of refraction, which sometimes leads to confusion. k is the extinction coefficient, which represents the damping of an EM wave inside the material. Both depend on the wavelength. An EM wave travels in the material with velocity v and angular frequency ω. The time-varying electric field of the wave is described by where only the real part of The index of refraction is defined to be the ratio of the speed of light in a vacuum to the speed of the EM wave in the medium: Substituting for Substituting this in the expression for the EM wave's electric field gives This expression describes a propagating electromagnetic wave with an exponentially damped amplitude due to the k term. This term causes the EM wave to "die out" as it travels further into the material. The intensity of the wave, which corresponds to the energy it carries with it, is simply the square of the magnitude of the wave's electric field. The intensity of the wave is therefore A law called the Beer-Lambert law states that in any medium that is absorbing light, the decrease in intensity I per unit length z is proportional to the instantaneous value of I. In mathematical form this is where α is the absorption coefficient of the material for that wavelength of EM radiation. This equation has the solution
where I0 is the intensity of the electromagnetic radiation at the surface of the absorbing medium. Comparing the two expressions for intensity obtained above gives Since c here denotes the speed of the EM wave in vacuum,
Substituting this in the expression above and rearranging shows that the extinction coefficient and the absorption coefficient are related by
where λ is the vacuum wavelength (not the wavelength of the EM wave in the material). See alsoReferences
Categories: Electromagnetic radiation | Spectroscopy |
|||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Opacity_(optics)". A list of authors is available in Wikipedia. |





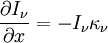 . The
. The 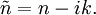
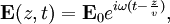
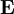 has physical significance. For simplicity, the radiation is assumed to be a plane wave, and its direction of propagation is denoted
has physical significance. For simplicity, the radiation is assumed to be a plane wave, and its direction of propagation is denoted 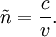
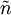 in the expression above gives
in the expression above gives
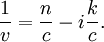
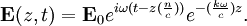
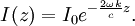
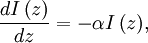
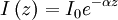 ,
,
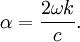
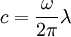 .
.
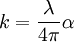 ,
,


