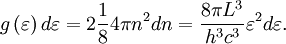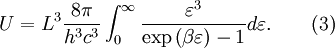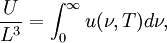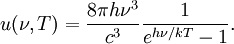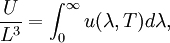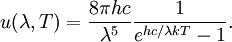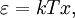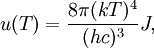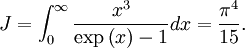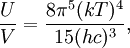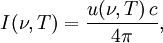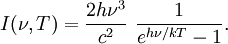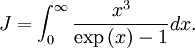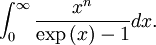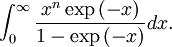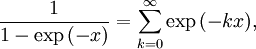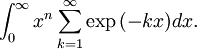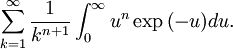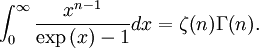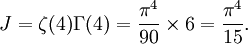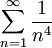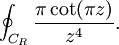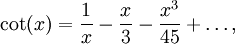To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Planck's lawFor a general introduction, see black body. In physics, Planck's law describes the spectral radiance of electromagnetic radiation at all wavelengths from a black body at temperature T. As a function of frequency ν, Planck's law is written as: As a function of wavelength λ it is written (for infinitesimal solid angle) as: Note that this formula will vary slightly by a constant factor (often a pi) depending on the field of view assumed in the derivation. Note also that the two functions have different units - the first is radiance per unit frequency interval while the second is radiance per unit wavelength interval. Hence, the quantities I(ν,T) and I(λ,T) are not equivalent to each other. To derive one from the other, they cannot simply be set equal to each other (ie: the expression for λ in terms of ν cannot just be substituted into the first equation to get the second). However, the two equations are related through: The following table provides the definition and SI units of measure for each symbol:
Product highlight
OverviewThe wavelength is related to the frequency by The law is sometimes written in terms of the spectral energy density[4] which has units of energy per unit volume per unit frequency (joule per cubic meter per hertz). Integrated over frequency, this expression yields the total energy density. The radiation field of a black body may be thought of as a photon gas, in which case this energy density would be one of the thermodynamic parameters of that gas. The spectral energy density can also be expressed as a function of wavelength: as shown in the derivation below. Max Planck originally produced this law in 1900 (published[5] in 1901) in an attempt to improve upon an expression proposed by Wilhelm Wien which fit the experimental data at short wavelengths but deviated from it at long wavelengths. He found that the above function, Planck's function, fitted the data for all wavelengths remarkably well. In constructing a derivation of this law, he considered the possible ways of distributing electromagnetic energy over the different modes of charged oscillators in matter. Planck's law emerged when he assumed that the energy of these oscillators was limited to a set of discrete, integer multiples of a fundamental unit of energy, E, proportional to the oscillation frequency ν: Planck made this quantization assumption five years before Albert Einstein hypothesized the existence of photons as a means of explaining the photoelectric effect. At the time, Planck believed that the quantization applied only to the tiny oscillators that were thought to exist in the walls of the cavity (what we now know to be atoms), and made no assumption that light itself propagates in discrete bundles or packets of energy. Moreover, Planck did not attribute any physical significance to this assumption, but rather believed that it was merely a mathematical device that enabled him to derive a single expression for the black body spectrum that matched the empirical data at all wavelengths. Although Planck's formula predicts that a black body will radiate energy at all frequencies, the formula is only applicable when many photons are being measured. For example, a black body at room temperature (300 kelvin) with one square meter of surface area will emit a photon in the visible range once about every thousand years or so, meaning that for most practical purposes, a black body at room temperature does not emit in the visible range. Ultimately, Planck's assumption of energy quantization and Einstein's photon hypothesis became the fundamental basis for the development of Quantum Mechanics. DerivationThe following derivation of Planck's law can be found, e.g., in [4]. See also the gas in a box article for a general derivation. Consider a cube of side L with conducting walls filled with electromagnetic radiation. At the walls of the cube, the parallel component of the electric field and the orthogonal component of the magnetic field must vanish. Analogous to the wave function of a particle in a box, one finds that the fields are superpositions of periodic functions. The three wavelengths λ1, λ2 and λ3, in the three directions orthogonal to the walls can be: where the ni are integers. For each set of integers ni there are two linear independent solutions (modes). According to quantum theory, the energy levels of a mode are given by: The quantum number r can be interpreted as the number of photons in the mode. The two modes for each set of ni correspond to the two polarization states of the photon which has a spin of 1. Note that for r = 0 the energy of the mode is not zero. This vacuum energy of the electromagnetic field is responsible for the Casimir effect. In the following we will calculate the internal energy of the box at temperature T relative to the vacuum energy. According to statistical mechanics, the probability distribution over the energy levels of a particular mode is given by: Here The denominator Z(β), is the partition function of a single mode and makes Pr properly normalized: Here we have defined which is the energy of a single photon. As explained here, the average energy in a mode can be expressed in terms of the partition function: This formula is a special case of the general formula for particles obeying Bose-Einstein statistics. Since there is no restriction on the total number of photons, the chemical potential is zero. The total energy in the box now follows by summing To calculate the density of states we rewrite equation (1) as follows: where n is the norm of the vector For every vector n with integer components larger or equal than zero there are two photon states. This means that the number of photon states in a certain region of n-space is twice the volume of that region. An energy range of Inserting this in Eq. (2) gives: From this equation one easily derives the spectral energy density as a function of frequency u(ν,T) and as a function of wavelength u(λ,T): where: u(ν,T) is known as the black body spectrum. It is a spectral energy density function with units of energy per unit frequency per unit volume. And: where This is also a spectral energy density function with units of energy per unit wavelength per unit volume. Integrals of this type for Bose and Fermi gases can be expressed in terms of polylogarithms. In this case, however, it is possible to calculate the integral in closed form using only elementary functions. Substituting in Eq. (3), makes the integration variable dimensionless giving: where J is given by: We prove this result in the Appendix below. The total electromagnetic energy inside the box is thus given by: where V = L3 is the volume of the box. (Note - This is not the Stefan-Boltzmann law, which is the total energy radiated by a black body. See that article for an explanation.) Since the radiation is the same in all directions, and propagates at the speed of light (c), the spectral intensity (energy/time/area/solid angle/frequency) is which yields HistoryMany popular science accounts of quantum theory, as well as some physics textbooks, contain some serious errors in their discussions of the history of Planck's Law. Although these errors were pointed out over forty years ago by historians of physics, they have proved to be difficult to eradicate. An article by Helge Kragh[6] gives a lucid account of what actually happened. Contrary to popular opinion, Planck did not quantize light. This is evident from his original 1901 paper [5] and the references therein to his earlier work. It is also plainly explained in his book "Theory of Heat Radiation," where he explains that his constant refers to Hertzian oscillators. The idea of quantization was developed by others into what we now know as quantum mechanics. The next step along this direction was made by Albert Einstein, who, by studying the photoelectric effect, proposed a model and equation whereby light was not only emitted but also absorbed in packets or photons. Then, in 1924, Satyendra Nath Bose developed the theory of the statistical mechanics of photons, which allowed a theoretical derivation of Planck's law. Contrary to another myth, Planck did not derive his law in an attempt to resolve the "ultraviolet catastrophe", the name given by Paul Ehrenfest to the paradoxical result that the total energy in the cavity tends to infinity when the equipartition theorem of classical statistical mechanics is applied to black body radiation. Planck did not consider the equipartion theorem to be universally valid, so he never noticed any sort of "catastrophe" — it was only discovered some five years later by Einstein, Lord Rayleigh, and Sir James Jeans. AppendixA simple way to calculate the integral is to calculate the general case first and then compute the answer at the end. Consider the integral Multiplying the numerator and denominator by exp( − x) gives us Since the denominator is always less than one, we can expand the denominator in powers of exp( − x) to get a convergent series Then we have Since each term in the sum represents a convergent integral, remove the summation out from under the integral sign. In addition, by a change of variable such that u = kx, we have The summation on the left is the Riemann zeta function ζ(n + 1), while the integral on the right is the Gamma function Γ(n + 1), and we are finally left with the general result For our problem, the numerator contains x3, leaving us with our specific result Here we have used that is the Riemann zeta function evaluated for the argument 4, which is given by π4 / 90. This fact can be proven by considering the contour integral Where CR is a contour of radius R around the origin. In the limit, as R approaches infinity, the integral approaches zero. Using the residue theorem the integral can also be written as a sum of residues at the poles of the integrand. The poles are at zero, the positive and negative integers. The sum of the residues yields precisely twice the desired summation plus the residue at zero. Because the integral approaches zero, the sum of all the residues must be zero. The summation must therefore equal minus one half times the residue at zero. From the series expansion of the cotangent function we see that the residue at zero is − π4 / 45 which yields the desired result. The evaluation of the Gamma function can be done by recognizing that for integral values of n, Γ(n + 1) = n!. In the appendix of the article Stefan-Boltzmann law we give a different derivation of this integral. (See also the integral of the Bose-Einstein distribution in the polylogarithm article.) Notes
References
Further readingPeter C. Milonni (1994). The Quantum Vacuum. Academic Press. Categories: Statistical mechanics | Foundational quantum physics |
||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Planck's_law". A list of authors is available in Wikipedia. |


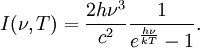
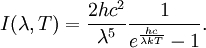
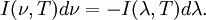
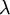
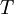
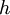
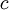
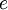
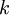



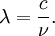
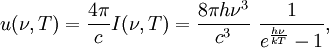
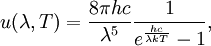
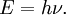
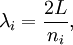
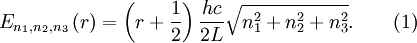
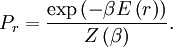
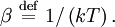
![Z\left(\beta\right)=\sum_{r=0}^{\infty}\exp\left[-\beta E\left(r\right)\right]=\frac{1}{1-\exp\left[-\beta\varepsilon\right]}.](images/math/5/e/3/5e3d0db7652f2a6ffc7117bd1425528b.png)
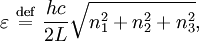
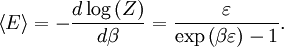
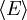 over all allowed single photon states. This can be done exactly in the thermodynamic limit as
over all allowed single photon states. This can be done exactly in the thermodynamic limit as 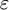 becomes continuous and we can then integrate
becomes continuous and we can then integrate 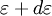 as
as 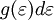 , where
, where 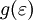 is the
is the 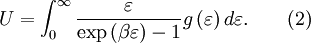
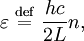
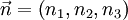 :
:
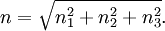
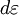 corresponds to shell of thickness
corresponds to shell of thickness 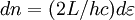 in n-space. Because the components of
in n-space. Because the components of 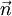 have to be positive, this shell spans an octant of a sphere. The number of photon states
have to be positive, this shell spans an octant of a sphere. The number of photon states 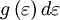 in an energy range
in an energy range