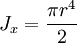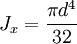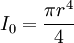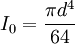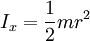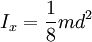To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Polar moment of inertiaPolar moment of inertia is a quantity used to predict an object's ability to resist torsion, in objects (or segments of objects) with an invariant circular cross-section and no significant warping or out-of-plane deformation.[1] It is used to calculate the twist of an object subjected to a torque. It is analogous to the area moment of inertia, which characterizes an object's ability to resist bending and is required to calculate displacement. The larger the polar moment of inertia, the less the beam will twist, when subjected to a given torque. The polar moment of inertia must not be confused with the moment of inertia, which characterizes an object's angular acceleration due to a torque. See moment (physics). Product highlight
LimitationsIn objects with significant cross-sectional variation, which cannot be analyzed in segments, and/or a non-circular cross-section a more complex approach has to be used. See 3-D elasticity. Definition
UnitThe SI unit for polar moment of inertia, like the area moment of inertia, is metre to the fourth power (m4) ApplicationThe polar moment of area appears in the formulae that describes torsional stress and angular displacement. Torsional stress: where T is the torque, r is the radius and Jx is the polar moment of area. In a circular shaft, the shear stress is maximal at the surface of the shaft (as that is where the torque is maximal): Most frequently the inverse problem is solved, in which one solves for the radius. Sample calculation
Calculation of the steam turbine shaft radius for a turboset: Assumptions:
The angular frequency can be calculated with the following formula:
The torque carried by the shaft is related to the power by the following equation:
The angular frequency is therefore 314.16 rad/s and the torque 3.1831 x 106 Nm. The maximal torque is: After substitution of the polar moment of inertia the following expression is obtained: The radius is 0.200 m. If one adds a factor of safety of 5 and re-calculates the radius with the maximal stress equal to the yield stress/5 the result is a radius of 0.343 m, or a diameter of 69 cm, the approximate size of a turboset shaft in a nuclear power plant. Comparing various moments of inertias for a cylinderPolar moment of inertiaor where:
Area moment of inertiaor Moment of inertiaor See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Polar_moment_of_inertia". A list of authors is available in Wikipedia. |





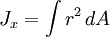
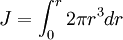
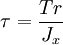
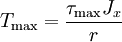
![r=\sqrt[3]{\frac{2 T_\max}{\pi {\tau}_\max}}](images/math/c/1/0/c1023a697a04b6bd610a5a389a0fa505.png)