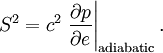To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Relativistic Euler equationsIn fluid mechanics and astrophysics, the relativistic Euler equations are a generalization of the Euler equations that account for the effects of special relativity. Product highlightThe equations of motion are contained in the continuity equation of the stress-energy tensor Tμν: where the right hand side is the zero tensor. For a perfect fluid,
Here e is the relativistic rest energy of the fluid, p is the fluid pressure, u is the four-velocity of the fluid, and ημν is the Minkowski metric tensor. To the above equations, a statement of conservation is usually added, usually conservation of baryon number. If n is the number density of baryons this may be stated These equations reduce to the classical Euler equations if The relativistic Euler equations may be applied to calculate the speed of sound in a fluid with a relativistic equation of state (that is, one in which the pressure is comparable with the internal energy density e, including the rest energy; e = ρc2 + ρeC where eC is the classical internal energy per unit mass). Under these circumstances, the speed of sound S is given by (note that
is the relativistic internal energy density). This formula differs from the classical case in that ρ has been replaced by e / c2.
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Relativistic_Euler_equations". A list of authors is available in Wikipedia. |





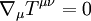
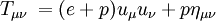 .
.
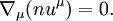
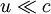 .
.