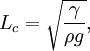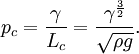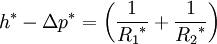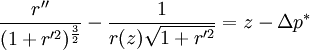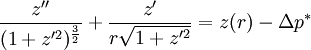To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Young–Laplace equationIn physics, the Young–Laplace equation is a nonlinear partial differential equation that describes the equilibrium pressure difference sustained across the interface between two static fluids, such as water and air, due to the phenomenon of surface tension. It relates the pressure difference to the shape of the surface and it is fundamentally important in the study of static capillary surfaces. It is a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface (zero thickness): where Δp is the pressure difference across the fluid interface, γ is the surface tension, The equation is named after Thomas Young, who developed the qualitative theory of surface tension in 1805, and Pierre-Simon Laplace who completed the mathematical description in the following year. It is sometimes also called the Young–Laplace–Gauss equation, as Gauss unified the work of Young and Laplace in 1830, deriving both the differential equation and boundary conditions using Johann Bernoulli's virtual work principles [2]. Product highlight
Soap filmsIf the pressure difference is zero, as in a soap film without gravity, the interface will assume the shape of a minimal surface. EmulsionsThe equation also explains the energy required to create an emulsion. To form the small, highly curved droplets of an emulsion, extra energy is required to overcome the large pressure that results from their small radius. Capillary pressure in a tubeIn a sufficiently narrow (ie, low Bond number) tube of circular cross-section (radius a), the interface between two fluids forms a meniscus in that is a portion of the surface of a sphere with radius R. The pressure jump across this surface is: This may be shown by writing the Young–Laplace equation in cylindrical form with a contact angle boundary condition and also a prescribed height boundary condition at, say, the bottom of the meniscus. The solution is a portion of a sphere, and the solution will exist only for the pressure difference shown above. This is significant because there isn't another equation or law to specify the pressure difference; existence of solution for one specific value of the pressure difference prescribes it. The radius of the sphere will be a function only of the contact angle, θ, which in turn depends on the exact properties of the fluids and the solids in which they are in contact: so that the pressure difference may be written as:
In order to maintain hydrostatic equilibrium, the induced capillary pressure is balanced by a change in height, h, which can be positive or negative, depending on whether the wetting angle is less than or greater than 90°. For a fluid of density ρ:
— where g is the gravitational acceleration. This is sometimes known as the Jurin rule or Jurin height[3] after James Jurin who studied the effect in 1718.[4] For a water-filled glass tube in air at sea level:
— and so the height of the water column is given by:
Thus for a 2 mm wide (1 mm radius) tube, the water would rise 14 mm. However, for a capillary tube with radius 0.1 mm, the water would rise 14 cm (about 6 inches). Capillary action in generalIn the general case, for a free surface and where there is an applied "over-pressure", Δp, at the interface then, in equilibrium, there is a balance between the applied pressure, the hydrostatic pressure and the effects of surface tension. The Young–Laplace equation becomes:
The equation can be non-dimensionalised in terms of its characteristic length-scale, the capillary length: — and characteristic pressure: For clean water at standard temperature and pressure, the capillary length is ~2 mm. The non-dimensional equation then becomes: Thus, the surface shape is determined by only one parameter, the over pressure of the fluid, Δp* and the scale of the surface is given by the capillary length. The solution of the equation requires an initial condition for position, and the gradient of the surface at the start point.
Axisymmetric equationsThe (nondimensional) shape, r(z) of an axisymmetric surface can be found by substituting general expressions for curvature to give the hydrostatic Young-Laplace equations: Application in medicineIn medicine it is often referred to as the Law of Laplace, and it is used in the context of respiratory physiology, in particular alveoli in the lung, where a single alveolus is modeled as being a perfect sphere.[5] In this context, the pressure differential is a force pushing inwards on the surface of the alveolus. The Law of Laplace states that there is an inverse relationship between surface tension and alveolar radius. It follows from this that a small alveolus will experience a greater inward force than a large alveolus, if their surface tensions are equal. In that case, if both alveoli are connected to the same airway, the small alveolus will be more likely to collapse, expelling its contents into the large alveolus. This explains why the presence of surfactant lining the alveoli is of vital importance. Surfactant reduces the surface tension on all alveoli, but its effect is greater on small alveoli than on large alveoli. Thus, surfactant compensates for the size differences between alveoli, and ensures that smaller alveoli do not collapse.[5] The Law of Laplace also explains various phenomena encountered in the pathology of vascular or gastrointestinal walls. The "surface tension" in this case represents the muscular tension on the wall of the vessel. For example, if an aneurysm forms in a blood vessel wall, the radius of the vessel has increased. This means that the inward force on the vessel decreases, and therefore the aneurysm will continue to expand until it ruptures. A similar logic applies to the formation of diverticuli in the gut.[6] HistoryFrancis Hauksbee performed some of the earliest observations and experiments in 1709 and these were repeated in 1718 by James Jurin who observed that the height of fluid in a capillary column was a function only of the cross-sectional area at the surface, not of any other dimensions of the column.[7][4] Thomas Young laid the foundations of the equation in his 1804 paper An Essay on the Cohesion of Fluids [8] where he set out in descriptive terms the principles governing contact between fluids (along with many other aspects of fluid behaviour). Pierre Simon Laplace followed this up in Mécanique Céleste [9] with the formal mathematical description given above, which reproduced in symbolic terms the relationship described earlier by Young. Laplace accepted the idea propounded by Hauksbee in the Philosophical Transactions for 1709, that the phenomenon was due to a force of attraction that was insensible at sensible distances. The part which deals with the action of a solid on a liquid and the mutual action of two liquids was not worked out thoroughly, but ultimately was completed by Gauss. Carl Neumann later filled in a few details.[10][7] References
Bibliography
|
|||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Young–Laplace_equation". A list of authors is available in Wikipedia. |


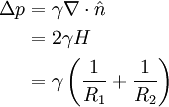
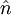 is a unit normal to the surface,
is a unit normal to the surface, 


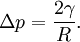
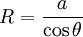
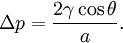
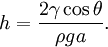 .
.
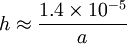
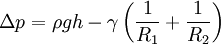 .
.