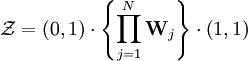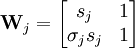To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Zimm-Bragg modelIn statistical mechanics, the Zimm-Bragg model is a helix-coil transition model that describes helix-coil transitions of macromolecules, usually polymer chains. Most models provide a reasonable approximation of the fractional helicity of a given polypeptide; the Zimm-Bragg model differs by incorporating the ease of propagation with respect to nucleation. Product highlight
Helix-coil transition modelsHelix-coil transition models assume that polypeptides are linear chains composed of interconnected segments. Further, models group these sections into two broad categories: coils, random conglomerations of disparate unbound pieces, are represented by the letter 'C', and helices, ordered states where the chain has assumed a structure stabilized by hydrogen bonding, are represented by the letter 'H'.[1] Thus, it is possible to loosely represent a macromolecule as a string such as CCCCHCCHCHHHHHCHCCC and so forth. The number of coils and helices factors into the calculation of fractional helicity, where
Zimm-Bragg
The Zimm-Bragg model takes the cooperativity of each segment into consideration when calculating fractional helicity. The probability of any given monomer being a helix or coil is affected by which the previous monomer is; that is, whether the new site is a nucleation or propagation. By convention, a coil unit ('C') is always of statistical weight 1. Addition of a helix state ('H') to a previously coiled state (nucleation) is assigned a statistical weight
Adding a helix state to a site that is already a helix (propagation) has a statistical weight of which makes the propagation of a helix more favorable than nucleation of a helix from coil state.[2] From these parameters, it is possible to compute the fractional helicity where
Statistical mechanicsThe Zimm-Bragg model is equivalent to a one-dimensional Ising model and has no long-range interactions, i.e., interactions between residues well separated along the backbone; therefore, by the famous argument of Rudolf Peierls, it cannot undergo a phase transition. The statistical mechanics of the Zimm-Bragg model[3] may be solved exactly using the transfer-matrix method. The two parameters of the Zimm-Bragg model are σ, the statistical weight for nucleating a helix and s, the statistical weight for propagating a helix. These parameters may depend on the residue j; for example, a proline residue may easily nucleate a helix but not propagate one; a leucine residue may nucleate and propagate a helix easily; whereas glycine may disfavor both the nucleation and propagation of a helix. Since only nearest-neighbour interactions are considered in the Zimm-Bragg model, the full partition function for a chain of N residues can be written as follows where the 2x2 transfer matrix Wj of the jth residue equals the matrix of statistical weights for the state transitions The row-column entry in the transfer matrix equals the statistical weight for making a transition from state row in residue j-1 to state column in residue j. The two states here are helix (the first) and coil (the second). Thus, the upper left entry s is the statistical weight for transitioning from helix to helix, whereas the lower left entry σs is that for transitioning from coil to helix. See also
References
Categories: Polymer physics | Protein structure | Statistical mechanics | Thermodynamics |
|||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Zimm-Bragg_model". A list of authors is available in Wikipedia. |





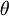 , defined as
, defined as
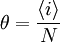
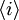 is the average helicity and
is the average helicity and
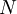 is the number of helix or coil units.
is the number of helix or coil units.
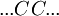
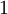
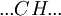
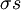
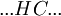
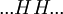
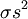
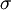 is the nucleation parameter and
is the nucleation parameter and
![s = \frac{[H]}{[C]}](images/math/5/c/c/5cca39ea0cc6eb03621c15841ff4e980.png) .
.
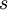 . For most
. For most 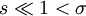
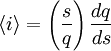
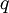 is the
is the 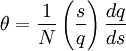 .
.