To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
AeroacousticsAeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. Although no complete scientific theory of the generation of noise by aerodynamic flows has been established, most practical aeroacoustic analysis relies upon the so-called Acoustic Analogy, whereby the governing equations of motion of the fluid are coerced into a form reminiscent of the wave equation of "classical" (i.e. linear) acoustics. The most common and a widely-used of the latter is Lighthill's aeroacoustic analogy. It was proposed by James Lighthill in the 1950s when noise generation associated with the jet engine was beginning to be placed under scientific scrutiny. Computational Aeroacoustics (CAA) is the application of numerical methods and computers to find approximate solutions of the governing equations for specific (and likely complicated) aeroacoustic problems. Product highlight
Lighthill's equationLighthill (1952) rearranged the Navier-Stokes equations, which govern the flow of a compressible viscous fluid, into an inhomogeneous wave equation, thereby making an analogy between fluid mechanics and acoustics. The first equation of interest is the conservation of mass equation, which reads where ρ and Next is the conservation of momentum equation, which is given by where p is the thermodynamic pressure, and σ is the viscous (or traceless) part of the stress tensor. Now, multiplying the conservation of mass equation by Note that Subtracting which is equivalent to where The above equation is the celebrated Lighthill equation of aeroacoustics. It is a wave equation with a source term on the right-hand side, i.e. an inhomogeneous wave equation. The argument of the "double-divergence operator" on the right-hand side of last equation, i.e. Using Einstein notation, Lighthill’s equation can be written as where and δij is the Kronecker delta. Each of the acoustic source terms, i.e. terms in Tij, may play a significant role in the generation of noise depending upon flow conditions considered. In practice, it is customary to neglect the effects viscosity of the fluid, i.e. one takes σ = 0, because it is generally accepted that the effects of the latter on noise generation, in most situations, are orders of magnitude smaller than those due to the other terms. Lighthill (1952) provides an in-depth discussion of this matter. In aeroacoustic studies, both theoretical and computational efforts are made to solve for the acoustic source terms in Lighthill's equation in order to make statements regarding the relevant aerodynamic noise generation mechanisms present. Finally, it is important to realize that Lighthill's equation is exact in the sense that no approximations of any kind have been made in its derivation. Related model equationsIn their classical text on fluid mechanics, Landau and Lifshitz (1987) derive an aeroacoustic equation analogous to Lighthill's (i.e., an equation for sound generated by "turbulent" fluid motion) but for the incompressible flow of an inviscid fluid. The inhomogeneous wave equation that they obtain is for the pressure p rather than for the density ρ of the fluid. Furthermore, unlike Lighthill's equation, Landau and Lifshitz's equation is not exact; it is an approximation. If one is to allow for approximations to be made, a simpler way (without necessarily assuming the fluid is incompressible) to obtain an approximation to Lighthill's equation is to assume that And for the case when the fluid is indeed incompressible, i.e. ρ = ρ0 (for some positive constant ρ0) everywhere, then we obtain exactly the equation given in Landau and Lifshitz (1987), namely A similar approximation [in the context of equation Of course, one might wonder whether we are justified in assuming that However, even after the above deliberations, it is still not clear whether one is justified in using an inherently linear relation to simplify a nonlinear wave equation. Nevertheless, it is a very common practice in nonlinear acoustics as the textbooks on the subject show: e.g., Naugolnykh and Ostrovsky (1998) and Hamilton and Morfey (1998). References
External references
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Aeroacoustics". A list of authors is available in Wikipedia. |





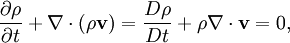
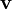 represent the density and velocity of the fluid, which depend on space and time, and
represent the density and velocity of the fluid, which depend on space and time, and 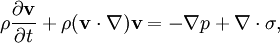
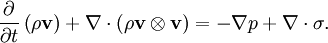
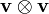 is a tensor (see also tensor product). Differentiating the conservation of mass equation with respect to time, taking the divergence of the conservation of momentum equation and subtracting the latter from the former, we arrive at
is a tensor (see also tensor product). Differentiating the conservation of mass equation with respect to time, taking the divergence of the conservation of momentum equation and subtracting the latter from the former, we arrive at
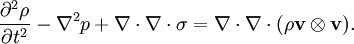
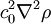 , where
, where ![\frac{\partial^2\rho}{\partial t^2}-c^2_0\nabla^2\rho = \nabla\cdot\left[\nabla\cdot(\rho\mathbf{v}\otimes\mathbf{v})-\nabla\cdot\sigma +\nabla p-c^2_0\nabla\rho\right],](images/math/c/b/7/cb7ec1c53d7350a8498f75347e2debbd.png)
![\frac{\partial^2\rho}{\partial t^2}-c^2_0\nabla^2\rho=(\nabla\otimes\nabla) :\left[\rho\mathbf{v}\otimes\mathbf{v} - \sigma + (p-c^2_0\rho)\mathbb{I}\right],](images/math/3/9/3/393319553b5da20b847f2209dceb5428.png)
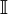 is the identity tensor, and
is the identity tensor, and 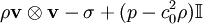 , is the so-called Lighthill turbulence stress tensor for the acoustic field, and it is commonly denoted by
, is the so-called Lighthill turbulence stress tensor for the acoustic field, and it is commonly denoted by 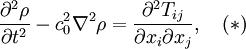
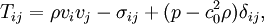
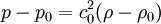 , where
, where 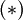 we obtain the equation
we obtain the equation
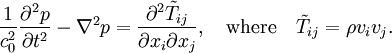
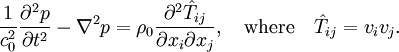
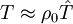 , is suggested by Lighthill (1952) [see Eq. (7) in the latter paper].
, is suggested by Lighthill (1952) [see Eq. (7) in the latter paper].
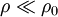 and
and 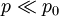 , then the assumed relation follows directly from the linear theory of sound waves (see, e.g., the linearized Euler equations and the acoustic wave equation). In fact, the approximate relation between
, then the assumed relation follows directly from the linear theory of sound waves (see, e.g., the linearized Euler equations and the acoustic wave equation). In fact, the approximate relation between 

