To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Born-Oppenheimer approximationIn quantum chemistry, the computation of the energy and wavefunction of an average-size molecule is a formidable task that is alleviated by the Born-Oppenheimer (BO) approximation. For instance the benzene molecule consists of 12 nuclei and 42 electrons. The time independent Schrödinger equation, which must be solved to obtain the energy and molecular wavefunction of this molecule, is a partial differential eigenvalue equation in 162 variables—the spatial coordinates of the electrons and the nuclei. The BO approximation makes it possible to compute the wavefunction in two less formidable, consecutive, steps. This approximation was proposed in the early days of quantum mechanics by Born and Oppenheimer (1927) and is still indispensable in quantum chemistry. In basic terms, it allows the wavefunction of a molecule to be broken into its nuclear, electronic and rotational components. Ψtotal = ψelectronicψvibrationalψrotational. In the first step of the BO approximation the electronic Schrödinger equation is solved, yielding the wavefunction ψelectronic depending on electrons only. For benzene this wavefunction depends on 126 electronic coordinates. During this solution the nuclei are fixed in a certain configuration, very often the equilibrium configuration. If the effects of the quantum mechanical nuclear motion are to be studied, for instance because a vibrational spectrum is required, this electronic computation must be repeated for many different nuclear configurations. The set of electronic energies thus computed becomes a function of the nuclear coordinates. In the second step of the BO approximation this function serves as a potential in a Schrödinger equation containing only the nuclei—for benzene an equation in 36 variables. The success of the BO approximation is due to the high ratio between nuclear and electronic masses. The approximation is an important tool of quantum chemistry, without it only the lightest molecule, H2, could be handled; all computations of molecular wavefunctions for larger molecules make use of it. Even in the cases where the BO approximation breaks down, it is used as a point of departure for the computations. The electronic energies, constituting the nuclear potential, consist of kinetic energies, interelectronic repulsions and electron-nuclear attractions. In a handwaving manner the nuclear potential is an averaged electron-nuclear attraction. The BO approximation follows from the inertia of electrons to be negligible in comparison to the atom to which they are bound. Product highlight
Short descriptionThe Born-Oppenheimer (BO) approximation is ubiquitous in quantum chemical calculations of molecular wavefunctions. It consists of two steps. In the first step the nuclear kinetic energy is neglected,[1] that is, the corresponding operator Tn is subtracted from the total molecular Hamiltonian. In the remaining electronic Hamiltonian He the nuclear positions enter as parameters. The electron-nucleus interactions are not removed and the electrons still "feel" the Coulomb potential of the nuclei clamped at certain positions in space. (This first step of the BO approximation is therefore often referred to as the clamped nuclei approximation.) The electronic Schrödinger equation is solved (out of necessity approximately). The quantity r stands for all electronic coordinates and R for all nuclear coordinates. Obviously, the electronic energy eigenvalue Ee depends on the chosen positions R of the nuclei. Varying these positions R in small steps and repeatedly solving the electronic Schrödinger equation, one obtains Ee as a function of R. This is the potential energy surface (PES): Ee(R) . Because this procedure of recomputing the electronic wave functions as a function of an infinitesimally changing nuclear geometry is reminiscent of the conditions for the adiabatic theorem, this manner of obtaining a PES is often referred to as the adiabatic approximation and the PES itself is called an adiabatic surface.[2] In the second step of the BO approximation the nuclear kinetic energy Tn (containing partial derivatives with respect to the components of R) is reintroduced and the Schrödinger equation for the nuclear motion[3] is solved. This second step of the BO approximation involves separation of vibrational, translational, and rotational motions. This can be achieved by application of the Eckart conditions. The eigenvalue E is the total energy of the molecule, including contributions from electrons, nuclear vibrations, and overall rotation and translation of the molecule. Derivation of the Born-Oppenheimer approximationIt will be discussed how the BO approximation may be derived and under which conditions it is applicable. At the same time we will show how the BO approximation may be improved by including vibronic coupling. To that end the second step of the BO approximation is generalized to a set of coupled eigenvalue equations depending on nuclear coordinates only. Off-diagonal elements in these equations are shown to be nuclear kinetic energy terms.
It will be shown that the BO approximation can be trusted whenever the PESs, obtained from the solution of
the electronic Schrödinger equation, are well separated: We start from the exact non-relativistic, time-independent molecular Hamiltonian: with The position vectors It is useful to introduce the total nuclear momentum and to rewrite the nuclear kinetic energy operator as follows: Suppose we have K electronic eigenfunctions The electronic wave functions which in general will not be zero. The total wave function with and where the subscript is diagonal. After multiplication by the real function is turned into a set of K coupled eigenvalue equations depending on nuclear coordinates only The column vector The vibronic coupling in this approach is through nuclear kinetic energy terms. Solution of these coupled equations gives an approximation for energy and wavefunction that goes beyond the Born-Oppenheimer approximation. Unfortunately, the off-diagonal kinetic energy terms are usually difficult to handle. This is why often a diabatic transformation is applied, which retains part of the nuclear kinetic energy terms on the diagonal, removes the kinetic energy terms from the off-diagonal and creates coupling terms between the adiabatic PESs on the off-diagonal. If we can neglect the off-diagonal elements the equations will uncouple and simplify drastically. In order to show when this neglect is justified, we suppress the coordinates in the notation and write, by applying the Leibniz rule for differentiation, the matrix elements of Tn as The diagonal (k' = k) matrix elements The matrix element in the numerator is The matrix element of the one-electron operator appearing on the right hand side is finite.
When the two surfaces come close, Conversely, if all surfaces are well separated, all off-diagonal terms can be neglected and hence the whole matrix of which are the normal second-step of the BO equations discussed above. We reiterate that when two or more potential energy surfaces approach each other, or even cross, the Born-Oppenheimer approximation breaks down and one must fall back on the coupled equations. Usually one invokes then the diabatic approximation. Historical noteThe Born-Oppenheimer approximation is named after M. Born and R. Oppenheimer who wrote a paper [Annalen der Physik, vol. 84, pp. 457-484 (1927)] entitled: Zur Quantentheorie der Molekeln (On the Quantum Theory of Molecules). This paper describes the separation of electronic motion, nuclear vibrations, and molecular rotation. Somebody who expects to find in this paper the BO approximation—as it is explained above and in most modern textboooks—will be in for a surprise. The reason being that the presentation of the BO approximation is well hidden in Taylor expansions (in terms of internal and external nuclear coordinates) of (i) electronic wave functions, (ii) potential energy surfaces and (iii) nuclear kinetic energy terms. Internal coordinates are the relative positions of the nuclei in the molecular equilibrium and their displacements (vibrations) from equilibrium. External coordinates are the position of the center of mass and the orientation of the molecule. The Taylor expansions complicate the theory and make the derivations very hard to follow. Moreover, knowing that the proper separation of vibrations and rotations was not achieved in this paper, but only 8 years later [by C. Eckart, Physical Review, vol. 46, pp. 383-387 (1935)] (see Eckart conditions), one is not very much motivated to invest much effort into understanding the work by Born and Oppenheimer, however famous it may be. Although the article still collects many citations each year, it is safe to say that it is not read anymore (except perhaps by historians of science). See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Born-Oppenheimer_approximation". A list of authors is available in Wikipedia. |





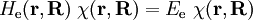
![\left[ T_\mathrm{n} + E_\mathrm{e}(\mathbf{R})\right] \phi(\mathbf{R}) = E \phi(\mathbf{R})](images/math/d/4/c/d4cd73f0fa40bdab7f1b828ba41bcf39.png)
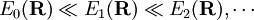 for all
for all 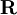 .
.
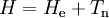
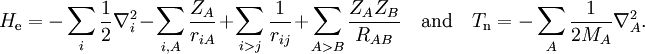
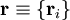 of the electrons and the position vectors
of the electrons and the position vectors 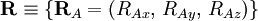 of the nuclei are with respect to a Cartesian inertial frame. Distances between particles are written as
of the nuclei are with respect to a Cartesian inertial frame. Distances between particles are written as 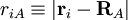 (distance between electron i and nucleus A) and similar definitions hold for
(distance between electron i and nucleus A) and similar definitions hold for 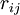 and
and 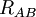 .
We assume that the molecule is in a homogeneous
(no external force) and isotropic (no external torque) space. The only interactions are the
Coulomb interactions between the electrons and nuclei. The Hamiltonian is expressed in
.
We assume that the molecule is in a homogeneous
(no external force) and isotropic (no external torque) space. The only interactions are the
Coulomb interactions between the electrons and nuclei. The Hamiltonian is expressed in 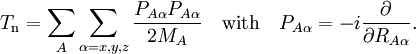
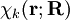 of
of 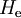 , that is, we have solved
, that is, we have solved
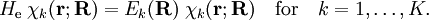
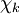 will be taken to be real, which is possible when there are no magnetic or spin interactions. The parametric dependence of the functions
will be taken to be real, which is possible when there are no magnetic or spin interactions. The parametric dependence of the functions 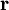 , its functional form depends on
, its functional form depends on 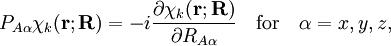
 is expanded in terms of
is expanded in terms of 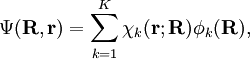
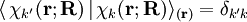
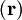 indicates that the integration, implied by the bra-ket notation,
is over electronic coordinates only. By definition, the matrix with general element
indicates that the integration, implied by the bra-ket notation,
is over electronic coordinates only. By definition, the matrix with general element
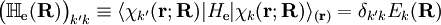
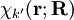 from the left and integration over the electronic coordinates
from the left and integration over the electronic coordinates 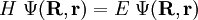
![\left[ \mathbb{H}_\mathrm{n}(\mathbf{R}) + \mathbb{H}_\mathrm{e}(\mathbf{R}) \right] \; \boldsymbol{\phi}(\mathbf{R}) = E\; \boldsymbol{\phi}(\mathbf{R}).](images/math/6/e/4/6e4b8bfca689e2048199a2916428c813.png)
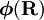 has elements
has elements 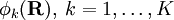 . The matrix
. The matrix 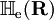 is diagonal and the nuclear Hamilton matrix is non-diagonal with the following off-diagonal (vibronic coupling) terms,
is diagonal and the nuclear Hamilton matrix is non-diagonal with the following off-diagonal (vibronic coupling) terms,
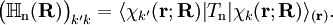
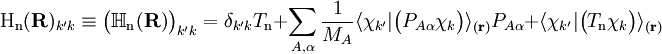
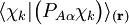 of the operator
of the operator 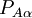 vanish, because this operator is Hermitian and purely imaginary. The off-diagonal matrix elements satisfy
vanish, because this operator is Hermitian and purely imaginary. The off-diagonal matrix elements satisfy
![\langle\chi_{k'}|\big(P_{A\alpha}\chi_k\big)\rangle_{(\mathbf{r})} = \frac{\langle\chi_{k'} |\big[P_{A\alpha}, H_\mathrm{e}\big] | \chi_k\rangle_{(\mathbf{r})}} {E_{k}(\mathbf{R})- E_{k'}(\mathbf{R})}.](images/math/e/b/0/eb0347ee357724859372c6b2f2b931c0.png)
![\langle\chi_{k'} |\big[P_{A\alpha}, H_\mathrm{e}\big] | \chi_k\rangle_{(\mathbf{r})} = iZ_A\sum_i \;\langle\chi_{k'}|\frac{(\mathbf{r}_{iA})_\alpha}{r_{iA}^3}|\chi_k\rangle_{(\mathbf{r})} \;\;\mathrm{with}\;\; \mathbf{r}_{iA} \equiv \mathbf{r}_i - \mathbf{R}_A .](images/math/5/9/7/597514c5661ee7687262985b7866c2eb.png)
 , the nuclear momentum coupling term becomes large and is no longer negligible. This is the case where
the BO approximation breaks down and a coupled set of nuclear motion equations must be considered, instead of the one equation appearing in the second step of the BO approximation.
, the nuclear momentum coupling term becomes large and is no longer negligible. This is the case where
the BO approximation breaks down and a coupled set of nuclear motion equations must be considered, instead of the one equation appearing in the second step of the BO approximation.
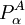 is effectively zero. The third term on the right hand side of the expression for the matrix element of Tn (the Born-Oppenheimer diagonal correction) can approximately be written as the matrix of
is effectively zero. The third term on the right hand side of the expression for the matrix element of Tn (the Born-Oppenheimer diagonal correction) can approximately be written as the matrix of ![\left[ T_\mathrm{n} +E_k(\mathbf{R})\right] \; \phi_k(\mathbf{R}) = E \phi_k(\mathbf{R}) \quad\mathrm{for}\quad k=1,\ldots, K,](images/math/e/9/7/e9774609b614a3c6e9e7bcae2ccb2b68.png)


