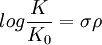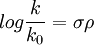Hammett equation

The basic idea is that for any two reactions with two aromatic reactants only differing in the type of substituent the change in free energy of activation is proportional to the change in Gibbs free energy ^[4]. This notion does not follow from elemental thermochemistry or chemical kinetics and was introduced by Hammett intuitively ^[5]

Additional recommended knowledge

Daily Sensitivity Test

Weighing the right way

Better weighing performance in 6 easy steps

Hammett equation

The basic equation is:

relating the equilibrium constant K for a given equilibrium reaction with substituent R and the reference K₀ constant with R=H to the substituent constant σ which depends only on the specific substituent R and the reaction constant ρ which depends only on the type of reaction but not on the substituent used.

The equation also holds for reaction rates k of a series of reactions with substituted benzene derivatives:

In this equation k₀ is the reference reaction rate of the unsubstituted reactant and k that of a substituted reactant.

A plot of log(K/K₀) for a given equilibrium versus log(k/k₀) for a given reaction rate with many differently substituted reactants will give a straight line.

Substituent constants

The starting point for the collection of the substituent constants is a chemical equilibrium for which both the substituent constant and the reaction constant are arbitrarily set to 1: the ionization of benzoic acid (R and R' both H) in water at 25°C.

Having obtained a value for K₀, a series of equilibrium constants (K) are now determined based on the same process but now with variation of the para substituent for instance p-Hydroxybenzoic acid (R=OH, R'=H) or 4-aminobenzoic acid (R=NH₂, R'=H). These values combined in the Hammett equation with K₀ and remembering that ρ = 1 give the para substituent constants compiled in table 1 for amine, methoxy, ethoxy, dimethylamino, methyl, fluorine, bromine, chlorine, iodine, nitro and cyano substituents. Repeating the process with meta-substituents afford the meta substituent constants. This treatment does not include ortho-substituents which would introduce steric effects.

The δ values displayed in table 1 ^[6] reveal certain substituent effects. With ρ = 1 the group of substituents with increasing positive values, notably cyano and nitro cause the equilibrium constant to increase compared to the hydrogen reference meaning that the acidity of the carboxylate anion (depicted on the right of the equation) has increased. These substituents stabilize the negative charge on the carboxylate oxygen atom by an electron-withdrawing inductive effect (-I) and also by a negative mesomeric effect (-M).

The next set of substituents are the halogens for which the substituent effect is still positive but much more modest. The reason for this is that while the inductive effect is still positive, the mesomeric effect is negative causing partial cancellation. The data also that for these substituents the meta effect is much larger than the para effect and this is due to the fact that the mesomeric effect is cancelled in a meta substituent.

This effect is depicted in scheme 3 where in a para substituted arene 1a, one resonance structure 1b is a quinoid with positive charge on the X substituent releasing electrons and thus destabilizing the Y substituent. This destabilizing effect is not possible when X has a meta orientation.

Other substituents like methoxy and ethoxy can even have opposite signs for the substituent constant as result of opposing inductive and mesomeric effect. Only alkyl and aryl substituents like methyl are electron-releasing in both respects.

Of course when the sign for the reaction constant is negative (next section) only substituents with a likewise negative substituent constant will increase equilibrium constants.

Reaction constants

With knowledge of substituent constants it is now possible to obtain reaction constants for a wide range of organic reactions. The archetypal reaction is the alkaline hydrolysis of ethyl benzoate (R=R'=H) in a water/ethanol mixture at 30°C. Measurement of the reaction rate k₀ combined with that of many substituted ethyl benzoates ultimately result in a reaction constant of +2.498 ^[2].

Reaction constants are known for many other reactions and equilibria, a selection of those provided by Hammett himself (with their values in parenthesis):

• the hydrolysis of substituted cinnamic acid ester in ethanol/water (+1.267)
• the ionization of substituted phenols in water (+2.008)
• the acid catalyzed esterification of substituted benzoic esters in ethanol (-0.085)
• the acid catalyzed bromination of substituted acetophenones (Ketone halogenation) in an acetic acid/water/hydrochloric acid (+0.417)
• the hydrolysis of substituted benzyl chlorides in acetone-water at 69.8°C (-1.875).

Reaction mechanisms and the value of ρ

Using benzoic acid ionization as a reference reaction, one can explore substituent effects on many other reactions. Knowing that benzoic acid creates a negative charge, and comparing substituent effects on the rate of reaction, one can determine the extent of charge developed. This is done by comparing the hammett plots of different reactions. To prepare a hammett plot one must simply measure the rates of reaction of differently substituted benzene analogues. Once these rates are obtained, the relative rates, or equilibrium constants, of the reaction compared to the unsubstituted compound (K_x/K_H, or k_x/k_H), are plotted against the substituent constant, σ, according to the Hammett equation.

The reaction constant, or sensitivity constant, ρ, describes the susceptibility of the reaction to subsituents, compared to the ionization of benzoic acid. It is equivalent to the slope of the Hammett plot. Information on the reaction and the associated mechanism can be obtained based on the value obtained for ρ. If the value of:

1. ρ>1, the reaction is more sensitive to substituents than benzoic acid and negative charge is built during the reaction.

2. 0<ρ<1 , the reaction is less sensitive to substituents than benzoic acid and negative charge is built.

3. ρ=0, no sensitivity to substituents, and no charge is built.

4. ρ<0, the reaction builds positive charge.

These relations can be exploited to elucidate the mechanism of a reaction. As the value of ρ is related to the charge during the rate determining step, mechanisms can be devised based on this information. If for example, the mechanism for the reaction of an aromatic compound is thought to occur through one of two mechanisms, the compound can be modified with substituents with different ρ values and kinetic measurements taken. Once these measurements have been made, a hammett plot can be constructed to determine the value of ρ. If one of these mechanisms involves the formation of charge, this can be verified based on the ρ value. Conversely, if the hammett plot shows that no charge is developed, i.e. a zero slope, the mechanism involving the building of charge can be discarded.

Hammett plots may not always be perfectly linear. For instance, a curve may show a sudden change in slope, or ρ value. In such a case, it is likely that the mechanism of the reaction changes upon adding a different substituent. Other deviations from linearity may be due to a change in the position of the transition state. In such a situation, certain substituents may cause the transition state to appear earlier (or later) in the reaction mechanism.^[7]

Hammett modifications

Other equations now exist that refine the original Hammett equation: the Swain-Lupton equation, the Taft equation and the Yukawa-Tsuno equation. An equation that address stereochemistry in aliphatic systems is also known ^[8].

See also

• Quantitative structure-activity relationship
• pKa
• Craig plot

References

1. ^ Definition IUPAC Gold Book 1996 Article
2. ^ ^{a b} The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives Louis P. Hammett J. Am. Chem. Soc.; 1937; 59(1); 96-103 Abstract
3. ^ Some Relations between Reaction Rates and Equilibrium Constants. Louis P. Hammett Chem. Rev.; 1935; 17(1); 125-136 Abstract
4. ^ Advanced Organic Chemistry Part A Second Edition F.A. Carey, R.J. Sundberg Plenum Press ISBN 0-306-41198-9
5. ^ The opening line in his 1935 publication reads: The idea that there is some sort of relationship between the rate of a reaction and the equilibrium constant is one of the most persistently held and at the same time most emphatically denied concepts in chemical theory
6. ^ These values are the original values obtained by Hammett in his1937 publication and may differ from subsequent publications by others. The following review contains more commonly accepted substituent constants: C. Hansch, A. Leo and R. W. Taft Chem. Rev.; 1991; 91; 165-195 Abstract
7. ^ Modern Physical Organic Chemistry E.V. Anslyn, D.A. Dougherty. University Science Books ISBN 1-891389-31-9
8. ^ M. Bols, X. Liang, H. H. Jensen “Equatorial contra axial polar substituents. The Relation of a Chemical Reaction to Stereochemical Substituent Constants.” J. Org. Chem. 2002; 67; 8970-74. Abstract