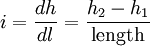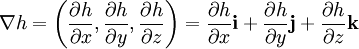To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hydraulic headHydraulic head is a specific measurement of water pressure or total energy per unit weight above a datum. It is usually measured as a water surface elevation, expressed in units of length, but represents the energy at the entrance (or bottom) of a piezometer. In an aquifer, it can be calculated from the depth to water in a piezometric well (a specialized water well), and given information of the piezometer's elevation and screen depth. Hydraulic head can similarly be measured in a column of water using a standpipe piezometer by measuring the height of the water surface in the tube relative to a common datum. In both cases, although the measurement is made at the water surface, the hydraulic head measurement represents the total energy at the entrance (base) of the piezometer. The hydraulic head can be used to determine a hydraulic gradient between two or more points. Product highlight
"Head" in fluid dynamicsIn fluid dynamics, head is the difference in elevation between two points in a column of fluid, and the resulting pressure of the fluid at the lower point. Head is normally expressed in units of height (e.g. meters), although some texts (incorrectly) refer to it in units of pressure such as pascals (the SI unit). Head refers to the constant right hand side in the incompressible steady version of Bernoulli's equation. This is best understood by considering a waterwheel: the head is the vertical distance from the top of the waterwheel to the free surface of the millpond. More generally, when considering a flow, one says that head is lost if energy is dissipated, often through turbulence; equations such as the Prony equation and the Darcy-Weisbach equation have been used to calculate the head loss due to friction. In the context of steam trains, one talks of a good head of steam, referring to the pressure in the boiler. The static head of a pump is the maximum height (pressure) it can deliver. The capacity of the pump can be read from its Q-H curve (flow vs. height). Head is used to describe the energy in incompressible fluids. Head has units of distance and equals the fluid's energy per unit weight. Head is useful in specifying centrifugal pumps because their pumping characteristics tend to be independent of the fluid's density. There are four types of head used to calculate the total head in and out of a pump:
Components of hydraulic headThe total hydraulic head is composed of pressure head, velocity head and elevation head. The pressure head is the equivalent gauge pressure of a column of water at the base of the piezometer, the velocity head is the kinetic energy from the motion of water, and the elevation head is the relative potential energy in terms of an elevation. This can be expressed as: where
In groundwater studies, the velocity head is assumed to be zero and is ignored. This is because groundwater moves very slowly, and the kinetic energy loss is very low. Thus, for groundwater studies, hydraulic head can be defined simply as: In an example with a 400 m deep piezometer, with an elevation of 1000 m, and a depth to water of 100 m: z = 600 m, ψ = 300 m, and h = 900 m. The pressure head can be expressed as: where
In faster moving water where the Reynolds number exceeds 10, such as in a river, the velocity head can be calculated using Bernoulli's principles as: where v is relative velocity of the water (distance per unit time, often m·s−1 or ft·s−1) Fresh water headThe pressure head is dependent on the density of water, which can vary depending on both the temperature and chemical composition (salinity, in particular). This means that the hydraulic head calculation is dependent on the density of the water within the piezometer. If one or more hydraulic head measurements are to be compared, they need to be standardized, usually to their fresh water head, which can be calculated as: where
Hydraulic gradientThe hydraulic gradient is a vector gradient between two or more hydraulic head measurements over the length of the flow path. It is also called the darcy slope, since it determines the quantity of a darcy flux, or discharge. A dimensionless hydraulic gradient can be calculated between two piezometers as: where
The hydraulic gradient can be expressed in vector notation, using the del operator. This requires a hydraulic head field, which can only be practically obtained from a numerical model, such as MODFLOW. In Cartesian coordinates, this can be expressed as: This vector describes the direction of the groundwater flow, where negative values indicate flow along the dimension, and zero indicates no flow. As with any other example in physics, energy must flow from high to low, which is why the flow is in the negative gradient. This vector can be used in conjunction with Darcy's law and a tensor of hydraulic conductivity to determine the flux of water in three dimensions. Hydraulic head in groundwaterThe distribution of hydraulic head through an aquifer determines where groundwater will flow. In a hydrostatic example (first figure), where the hydraulic head is constant, there is no flow. However, if there is a difference in hydraulic head from the top to bottom due to draining from the bottom (second figure), the water will flow downward, due to the difference in head, also called the hydraulic gradient. Atmospheric pressureEven though it is convention to use gauge pressure in the calculation of hydraulic head, it is more correct to use total pressure (gauge pressure + atmospheric pressure), since this is truly what drives groundwater flow. Often detailed observations of barometric pressure are not available at each well through time, so this is often disregarded (contributing to large errors at locations where hydraulic gradients are low or the angle between wells is acute.) The effects which changes in atmospheric pressure have water levels observed in wells has been known for many years. The effect is a direct one, an increase in atmospheric pressure is an increase in load on the water in the aquifer, which increases the depth to water (lowers the water level elevation). Pascal first qualitatively observed these effects in the 1600s, and they were more rigorously described by the soil physicist Edgar Buckingham (working for the USDA) using air flow models in 1907. Analogs to other fieldsHydraulic head is a measure of energy, and has many analogs in physics and chemistry, where the same mathematical principles and rules apply:
See also
References
|
|||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hydraulic_head". A list of authors is available in Wikipedia. |





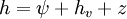
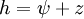
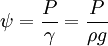
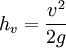
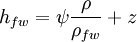
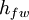 is the fresh water head (Length, measured in m or ft), and
is the fresh water head (Length, measured in m or ft), and
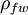 is the
is the