To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Nanofluidics
When structures approach the size regime corresponding to molecular scaling lengths, new physical constraints are placed on the behavior of the fluid. For example, these physical constraints induce regions of the fluid to exhibit new properties not observed in bulk, e.g. vastly increased viscosity near the pore wall; they may effect changes in thermodynamic properties and may also alter the chemical reactivity of species at the fluid-solid interface. A particularly relevant and useful example is displayed by electrolyte solutions confined in nanopores that contain surface charges, i.e. at electrified interfaces, as shown in the nanocapillary array membrane (NCAM) in the accompanying figure. All electrified interfaces induce an organized charge distribution near the surface known as the electrical double layer. In pores of nanometer dimensions the electrical double layer may completely span the width of the nanopore, resulting in dramatic changes in the composition of the fluid and the related properties of fluid motion in the structure. For example, the drastically enhanced surface-to-volume ratio of the pore results in a preponderance of counter-ions (i.e. ions charged oppositely to the static wall charges) over co-ions (possessing the same sign as the wall charges), in many cases to the near-complete exclusion of co-ions, such that only one ionic species exists in the pore. This can be used for manipulation of species with selective polarity along the pore length to achieve unusual fluidic manipulation schemes not possible in micrometer and larger structures. Product highlight
TheoryIn 1965, Rice and Whitehead published the seminal contribution to the theory of the transport of electrolyte solutions in long (ideally infinite) nanometer-diameter capillaries.[1]
Briefly, the potential, ϕ, at a radial distance, r, is given by the Poisson-Boltzmann equation,
FabricationNanostructures can be fabricated as single cylindrical channels, nanoslits, or nanochannel arrays from materials such as silicon, glass, polymers (e.g PMMA, PDMS, PCTE) and synthetic vesicles.[2] Standard photolithography, bulk or surface micromachining, replication techniques (embossing, printing, casting and injection molding), and nuclear track or chemical etching,[3][4] are commonly used to fabricate structures which exhibit characteristic nanofluidic behavior. ApplicationsBecause of the small size of the fluidic conduits, nanofluidic structures are naturally applied in situations demanding that samples be handled in exceedingly small quantities, including Coulter counting,[5] analytical separations and determinations of biomolecules, such as proteins and DNA,[6] and facile handling of mass-limited samples. One of the more promising areas of nanofluidics is its potential for integration into microfluidic systems, i.e. MicroTotal Analytical Systems or Lab-on-a-chip structures. For instance, NCAMs, when incorporated into microfluidic devices, can reproducibly perform digital switching, allowing transfer of fluid from one microfluidic channel to another,[7] selectivity separate and transfer analytes by size and mass,[7][8][9][10][11], mix reactants efficiently,[12] and separate fluids with disparate characteristics.[7][13] In addition, there is a natural analogy between the fluid handling capabilities of nanofluidic structures and the ability of electronic components to control the flow of electrons and holes. This analogy has been used to realize active electronic functions such as rectification[14] and field-effect[15][16] and bipolar transistor[17][18] action with ionic currents. Because the science of nanofluidics is still in its infancy, we can expect rapid development of new applications in the coming years. See alsoReferences
Categories: Nanotechnology | Fluid dynamics | Analytical chemistry | Surface chemistry | Materials science |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Nanofluidics". A list of authors is available in Wikipedia. |





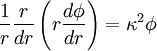
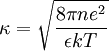
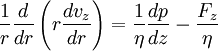
![v_z\left (r \right) = \frac{\epsilon \phi_0}{4 \pi \eta} E_z \left [ 1 - \frac {I_0 \left ( \kappa r \right )} {I_0 \left ( \kappa a \right )} \right ]](images/math/1/6/9/16935d773bdf514a2277e616675db951.png)


