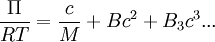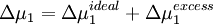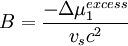Theta solvent

In a polymer solution, a theta solvent (or θ solvent) is a solvent in which polymer coils act like ideal chains, assuming exactly their random walk coil dimensions. Thermodynamically, the excess chemical potential of mixing between a polymer and a theta solvent is zero.

Additional recommended knowledge

How to ensure accurate weighing results every day?

Essential Laboratory Skills Guide

What is the Correct Way to Check Repeatability in Balances?

Physical Interpretation

The conformation assumed by a polymer chain in dilute solution can be modeled as a random walk of monomer subunits using a freely jointed chain model. However, this model does not account for steric effects. Real polymer coils are more closely represented by a self-avoiding walk because conformations in which different chain segments occupy the same space are not physically possible. This “excluded volume” effect causes the polymer to expand.

Chain conformation is also affected by solvent quality. The intermolecular interactions between polymer chain segments and coordinated solvent molecules have an associated energy of interaction which can be positive or negative. If a solvent is “good,” interactions between polymer segments and solvent molecules are energetically favorable, and will cause polymer coils to expand. If a solvent is “poor,” polymer-polymer self-interactions are preferred, and the polymer coils will contract. The quality of the solvent depends on both the chemical compositions of the polymer and solvent molecules and the solution temperature.

If a solvent is precisely poor enough to cancel the effects of excluded volume expansion, the “theta (θ) condition” is satisfied. For a given polymer-solvent pair, the theta condition is satisfied at a certain temperature, called the “theta (θ) temperature.” A solvent at this temperature is called a theta solvent.

In general, measurements of the properties of polymer solutions depend on the solvent. However, when a theta solvent is used, the measured characteristics are independent of the solvent. They depend only on short-range properties of the polymer such as the bond length, bond angles, and sterically favorable rotations. The polymer chain will behave exactly as predicted by the random walk or ideal chain model. This makes experimental determination of important quantities such as the root mean square end-to-end distance or the radius of gyration much simpler.

Additionally, the theta condition is also satisfied in the bulk amorphous polymer phase. Thus, the conformations adopted by polymers dissolved in theta solvents are identical to those adopted in bulk polymer.

Thermodynamic Definition

Thermodynamically, the excess chemical potential of mixing between a polymer and theta solvent is zero. Equivalently, the Gibbs free energy of mixing is ideal.

The chemical potential cannot be measured by any direct means, but it can be correlated to the osmotic pressure, Π, of the solution and the partial specific volume, v_s, of the solvent:

Δμ₁ = − v_sΠ

The concentration dependence of the osmotic pressure can be written as a virial expansion,

where M is the molecular weight of the polymer, R is the gas constant, T is the absolute temperature, and B is the second virial coefficient. Because the change in the chemical potential upon mixing is made up of an ideal term and an excess term,

the second virial coefficient, B, is proportional to the excess chemical potential of mixing:

This parameter reflects the energy of binary interactions between polymer chain segments and solvent molecules. When B > 0, the solvent is “good,” and when B < 0, the solvent is “poor.” For a theta solvent, the second virial coefficient is equal to zero because the excess chemical potential is zero by definition. A solvent at its theta temperature is in this respect analogous to a real gas at its Boyle temperature.

This relationship with osmotic pressure provides one means by which the theta condition (ie. the theta temperature for a particular solvent) can be determined. Similar relationships exist for other experimental techniques including light scattering, intrinsic viscosity measurement, sedimentation equilibrium, and cloud point titration.

References

^{[1] [2] [3] [4]}

1. ^ Hiemenz, Paul; Timothy Lodge (2007). Polymer Chemistry. Boca Raton, Florida: CRC Press. ISBN 1-57444-779-3. 
2. ^ Elias, Hans (2003-04-15). Theta Solvents. Wiley Database of Polymer Properties. John Wiley & Sons. Retrieved on 2007-12-12.
3. ^ Flory, Paul (1974-12-11). Spatial Configuration of Macromolecular Chains (PDF). Naubel Lecture. Retrieved on 2007-12-12.
4. ^ Sundararajan, P (2006). "Theta Temperatures". Physical Properties of Polymers Handbook. Ed. James Mark. New York, New York: Springer. Retrieved on 2007-12-12. 

See also

• Flory-Huggins solution theory