To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Upper Convected Maxwell modelThe Upper Convected Maxwell model (or UCM model) is a generalisation of the Maxwell material for the case of large deformations using the Upper convected time derivative. The model was proposed by J. G. Oldroyd. The model can be written as: where:
Product highlight
Case of the Steady ShearFor this case only two components of the shear stress became non-zero: and where Thus, the Upper Convected Maxwell model predicts for the simple shear that shear stress to be proportional to the shear rate and the first difference of normal stresses (T11 − T22) is proportional to the square of the shear rate, the second difference of normal stresses (T22 − T33) is always zero. In other words, UCM predicts appearance of the first difference of normal stresses but does not predict non-Newtonian behavior of the shear viscosity nor the second difference of the normal stresses. Usually quadratic behavior of the first difference of normal stresses and no second difference of the normal stresses is a realistic behavior of polymer melts at moderated shear rates, but constant viscosity is unrealistic and limits usability of the model. Case of start-up of Steady ShearFor this case only two components of the shear stress became non-zero: and The equations above describe stresses gradually risen from zero the steady-state values. The equation is only applicable, when the velocity profile in the shear flow is fully developed. Then the shear rate is constant over the channel height. If the start-up form a zero velocity distribution has to be calculated, the full set of PDEs has to be solved. Case of the Steady State Uniaxial Extension or Uniaxial CompressionFor this case UCM predicts the normal stresses σ = T11 − T22 = T11 − T33 calculated by the following equation: where The equation predicts the elongation viscosity approaching 3η0 (the same as for the Newtonian fluids) for the case of low elongation rate ( Case of small deformationFor the case of small deformation the nonlinearities introduced by the Upper Convected Derivative disappear and the model became an ordinary model of Maxwell material. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Upper_Convected_Maxwell_model". A list of authors is available in Wikipedia. |


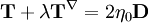
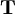 is the
is the 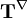 is the
is the 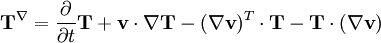
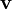 is the fluid velocity
is the fluid velocity
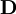 is the tensor of the deformation rate.
is the tensor of the deformation rate.



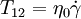
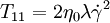
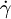 is the shear rate.
is the shear rate.
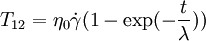
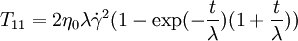
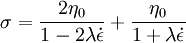
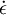 is the elongation rate.
is the elongation rate.
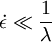 ) with fast deformation thickening with the steady state viscosity approaching infinity at some elongational rate (
) with fast deformation thickening with the steady state viscosity approaching infinity at some elongational rate (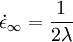 ) and at some compression rate (
) and at some compression rate (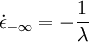 ). This behavior seems to be realistic.
). This behavior seems to be realistic.


