Entanglement bonanza
Relatively simple quantum computers could be much more powerful than previously realized.
quantum computers promise huge speedups on some computational problems because they harness a strange physical property called entanglement, in which the physical state of one tiny particle depends on measurements made of another. In quantum computers, entanglement is a computational resource, roughly like a chip’s clock cycles — kilohertz, megahertz, gigahertz — and memory in a conventional computer.
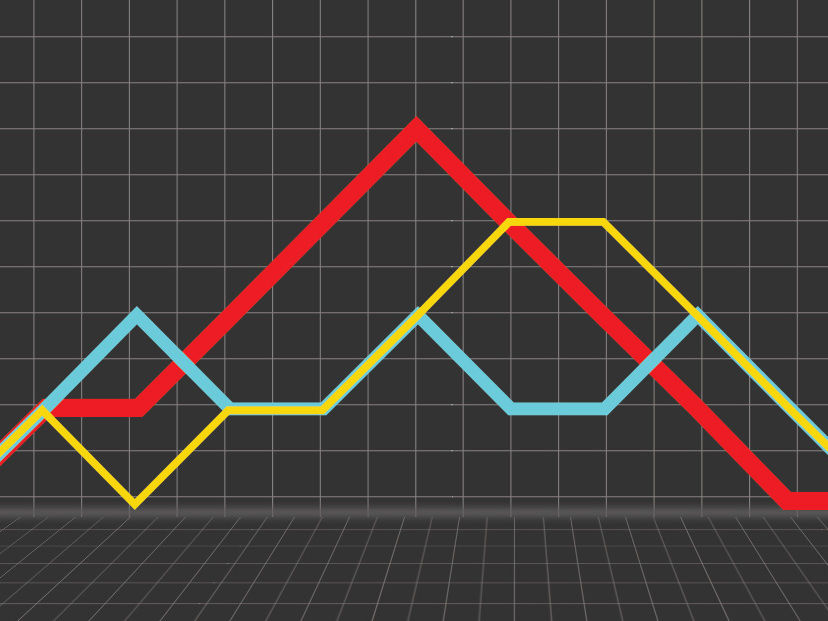
In this illustration, each colored line represents a different state of a “spin chain,” which can be thought of as the magnetic orientations, or spins, of a string of quantum particles. Where the line rises, the spin is up; where it falls, the spin is down; and where it’s flat, the spin is zero. MIT researchers modeled the entanglement of a quantum system as the “superposition” of such states.
Illustration: Christine Daniloff/MIT
Researchers at MIT and IBM’s Thomas J. Watson Research Center show that simple systems of quantum particles exhibit exponentially more entanglement than was previously believed. That means that quantum computers — or other quantum information devices — powerful enough to be of practical use could be closer than we thought.
Where ordinary computers deal in bits of information, quantum computers deal in quantum bits, or qubits. Previously, researchers believed that in a certain class of simple quantum systems, the degree of entanglement was, at best, proportional to the logarithm of the number of qubits.
“For models that satisfy certain physical-reasonability criteria — i.e., they’re not too contrived; they’re something that you could in principle realize in the lab — people thought that a factor of the log of the system size was the best you can do,” says Ramis Movassagh, a researcher at Watson and one of the paper’s two co-authors. “What we proved is that the entanglement scales as the square root of the system size. Which is really exponentially more.”
That means that a 10,000-qubit quantum computer could exhibit about 10 times as much entanglement as previously thought. And that difference increases exponentially as more qubits are added.
Logical or physical?
This matters because of the distinction, in quantum computing, between logical qubits and physical qubits. A logical qubit is an abstraction used to formulate quantum algorithms; a physical qubit is a tiny bit of matter whose quantum states are both controllable and entangled with those of other physical qubits.
A computation involving, say, 100 logical qubits would already be beyond the capacity of all the conventional computers in the world. But with most of today’s theoretical designs for general-purpose quantum computers, realizing a single logical qubit requires somewhere around 100 physical qubits. Most of the physical qubits are used for quantum error correction and to encode operations between logical qubits.
Since preserving entanglement across large groups of qubits is the biggest obstacle to developing working quantum devices, extracting more entanglement from smaller clusters of qubits could make quantum computing devices more practical.
Qubits are analogous to bits in a conventional computer, but where a conventional bit can take on the values 0 or 1, a qubit can be in “superposition,” meaning that it takes on both values at once. If qubits are entangled, they can take on all their possible states simultaneously. One qubit can take on two states, two qubits four, three qubits eight, four qubits 16, and so on. It’s the ability to, in some sense, evaluate computational alternatives simultaneously that gives quantum computers their extraordinary power.
In the new paper, Peter Shor, the Morss Professor of Applied Mathematics at MIT, and Movassagh, who completed his PhD with Shor at MIT, analyze systems of qubits called spin chains. In quantum physics, “spin” describes the way a bit of matter — it could be an electron, or an atom, or a molecule — orients itself in a magnetic field. Shor and Movassagh consider bits of matter with five possible spin states: two up states, two corresponding down states, and a zero, or flat, state.
Previously, theorists had demonstrated strong entanglement in spin chains whose elements had 21 spin states and interacted with each other in complex ways. But such systems would be extremely difficult to build in the lab.
Chain, chain, chain
A spin chain can be envisioned as a sequence of particles lined up next to each other. Interactions between the spins of adjacent particles determine the total energy of the system.
Shor and Movassagh first considered the set of all possible orientations of their spin chain whose net energy was zero. That means that if somewhere there was a spin up, of either of the two types, somewhere there had to be a corresponding spin down.
Then they considered the superposition of all those possible states of the spin chain. But the major breakthrough of the paper was to convert that superposition into the lowest-energy state of a Hamiltonian.
A Hamiltonian is a matrix — a big grid of numbers — that figures in the standard equation for describing the evolution of a quantum system. For any given state of the particles in the system, the Hamiltonian provides the system’s total energy.
In the previous 30 years, Movassagh says, no one had found an example of a Hamiltonian whose lowest-energy state corresponded to a system with as much entanglement as his and Shor’s exhibits. And even for Shor and Movassagh, finding that Hamiltonian required a little bit of luck.
“Originally, we wanted to prove a different problem,” Movassagh says. “We tried to come up with a model that proved some other theorem on generic aspects of entanglement, and we kept failing. But by failing, our models became more and more interesting. At some point, these models started violating this log factor, and they took on a life of their own.”
Pros and cons
“It’s a beautiful result, a beautiful paper,” says Israel Klich, an associate professor of physics at the University of Virginia. “It certainly made for a lot of interest in some parts of the physics community. The result is in fact very, very succinct and simple. It’s a relatively simple Hamiltonian whose ground state one can understand by simple combinatorial means.”
“Inspired by this work, we recently introduced a new variation on this model that is even more entangled, which has, actually, linear scaling of entanglement,” Klich adds. “The reason this was possible is that if you look at the ground state wave function, it’s so easy to understand how entanglement builds up there, and that gave us the idea of how to string it on to be even more entangled.”
But John Cardy, an emeritus professor of physics at Oxford University and a visiting professor at the University of California at Berkeley, doesn’t find the MIT researchers’ Hamiltonian so simple. “If you read the description of the Hamiltonian, it takes a lot of description,” he says. “When we have physically reasonable Hamiltonians, we can just write them down in one expression. They do have an equation that tells you what the Hamiltonian is. But to explain what all those ingredients are requires this whole formalism of these Markov chains and that kind of thing, that are deliberately designed, as far as I can tell, to get the result that they want.”
“But I don’t want to sound unduly negative, because this is the way that science proceeds,” he adds. “You find one counterexample, then you might find others that are more reasonable.”
Original publication
Other news from the department science
Get the chemical industry in your inbox
From now on, don't miss a thing: Our newsletter for the chemical industry, analytics, lab technology and process engineering brings you up to date every Tuesday and Thursday. The latest industry news, product highlights and innovations - compact and easy to understand in your inbox. Researched by us so you don't have to.
