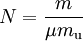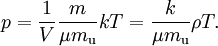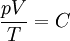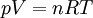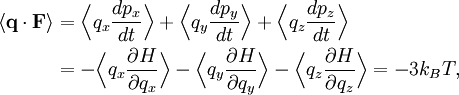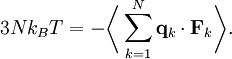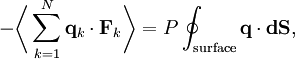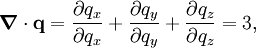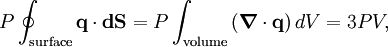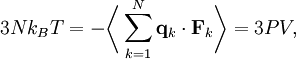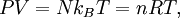To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ideal gas lawThe ideal gas law is the equation of state of a hypothetical ideal gas, first stated by Benoît Paul Émile Clapeyron in 1834.
where
The appropriate value of the ideal gas constant (R) depends on the units being used. In SI units, R = 8.314 472 J mol-1 K-1 (or equivalently m3 Pa K−1 mol−1). Other useful values for R are: The ideal gas law mathematically follows from a statistical mechanical treatment of primitive identical particles (point particles without internal structure) which do not interact, but exchange momentum (and hence kinetic energy) in elastic collisions. Since it neglects both molecular size and intermolecular attractions, the ideal gas law is most accurate for monoatomic gases at high temperatures and low pressures. Obviously the neglect of molecular size becomes less important for larger volumes, i.e., for lower pressures. The relative importance of intermolecular attractions diminishes with increasing thermal kinetic energy i.e., with increasing temperatures. More sophisticated equations of state, such as the van der Waals equation, allow deviations from ideality caused by molecular size and intermolecular forces to be taken into account. Additional recommended knowledge
Alternative formsAs the amount of substance could be given in mass instead of moles, sometimes an alternative form of the ideal gas law is useful. The number of moles ( Then, replacing from where
This form of the ideal gas law is particularly useful because it links pressure, density ρ = m / V, and temperature in a unique formula independent from the quantity of the considered gas. In statistical mechanics the following molecular equation is derived from first principles: Here From here we can notice that for an average particle mass of μ times the atomic mass constant mu (i.e., the mass is μ u) and since ρ = m / V, we find that the ideal gas law can be re-written as: DerivationsEmpiricalThe ideal gas law can be derived from combining two empirical gas laws: the combined gas law and Avogadro's law. The combined gas law states that where C is a constant which is directly proportional to the amount of gas, n (Avogadro's law). The proportionality factor is the universal gas constant, R, i.e. C = nR. Hence the ideal gas law
TheoreticalThe ideal gas law can also be derived from first principles using the kinetic theory of gases, in which several simplifying assumptions are made, chief among which are that the molecules, or atoms, of the gas are point masses, possessing mass but no significant volume, and undergo only elastic collisions with each other and the sides of the container in which both linear momentum and kinetic energy are conserved. Derivation from the statistical mechanicsLet q = (qx, qy, qz) and p = (px, py, pz) denote the position vector and momentum vector of a particle of an ideal gas,respectively, and let F denote the net force on that particle, then where the first equality is Newton's second law, and the second line uses Hamilton's equations and the equipartition theorem. Summing over a system of N particles yields
where dS is the infinitesimal area element along the walls of the container. Since the divergence of the position vector q is the divergence theorem implies that where dV is an infinitesimal volume within the container and V is the total volume of the container. Putting these equalities together yields which immediately implies the ideal gas law for N particles: where n=N/NA is the number of moles of gas and R=NAkB is the gas constant. See alsoReferences
Categories: Gas laws | Thermodynamics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ideal_gas_law". A list of authors is available in Wikipedia. |


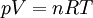
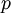 is the absolute
is the absolute 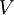 is the volume of the vessel,
is the volume of the vessel,
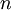 is the
is the 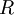 is the ideal gas constant,
is the ideal gas constant,
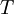 is the absolute temperature.
is the absolute temperature.



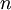 ) is equal to the mass (
) is equal to the mass (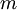 ) divided by the
) divided by the 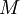 ):
):
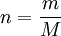
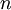 gives:
gives:
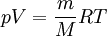
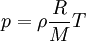 .
.
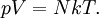
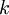 is
is 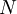 is the actual number of molecules, in contrast to the other formulation, which uses
is the actual number of molecules, in contrast to the other formulation, which uses 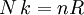 , and the consistency of this result with experiment is a good check on the principles of statistical mechanics.
, and the consistency of this result with experiment is a good check on the principles of statistical mechanics.