My watch list

Lapse rate

The lapse rate is defined as the negative of the rate of change in an atmospheric variable, usually temperature, with height observed while moving upwards through an atmosphere.^[1]^[2] While typically applied to Earth's atmosphere, the concept can be extended to any gravitationally supported ball of gas.

Additional recommended knowledge

Better weighing performance in 6 easy steps

What is the Sensitivity of my Balance?

Definition

A formal, peer-reviewed definition from the Glossary of Meteorology^[3] is:

The decrease of an atmospheric variable with height, the variable being temperature, unless otherwise specified.

The term applies ambiguously to the environmental lapse rate and the process lapse rate, and the meaning must often be ascertained from the context.

Types of lapse rates

There are two types of lapse rate:

Environmental lapse rate - which refers to the actual change of temperature with altitude for the stationary atmosphere (i.e. the temperature gradient)
The adiabatic lapse rates - which refer to the change in temperature of a mass of air as it moves upwards. There are two adiabatic rates:^[4]
- Dry adiabatic lapse rate
- Moist adiabatic lapse rate

Environmental lapse rate

The environmental lapse rate (ELR), is the negative of the actual change of temperature with altitude of the stationary atmosphere at a specific time and specific location. The ELR at a given place varies from day to day and even during each day. As an average the International Civil Aviation Organization (ICAO) defines an international standard atmosphere with a temperature lapse rate of 6.49 °C/1000 m (3.56 °F or 1.98 °C/1000 ft) from sea level to 11 km (36,090 ft). From 11 km (36,090 ft or 6.8 mi) up to 20 km (65,620 ft or 12.4 mi), the constant temperature is -56.5 °C (-69.7 °F), which is the lowest assumed temperature in ISA. It is important to remember that the standard atmosphere contains no moisture, and that the temperature of the atmosphere does not always fall steadily. For example there can be an inversion layer in which the temperature rises with increasing height.

Dry adiabatic lapse rate

The dry adiabatic lapse rate (DALR) is the negative of the rate at which a rising parcel of dry or unsaturated air changes temperature with increasing height, under adiabatic conditions. Unsaturated air has less than 100% relative humidity, i.e. its temperature is higher than its dew point. The term adiabatic means that no heat transfer (energy transfer due to a temperature difference) occurs into or out of the parcel. Air has low thermal conductivity, and the bodies of air involved are very large, so transfer of heat by conduction is negligibly small.

Under these conditions, when the air is stirred (for instance, by convection), and a parcel of air rises, it expands, because the pressure is lower at higher altitudes. As the air parcel expands, it pushes on the air around it, doing work; since the parcel does work and gains no heat, it loses internal energy, and so its temperature decreases. (The reverse occurs for a sinking parcel of air.)^[5]

For an ideal gas, the equation relating temperature T and pressure p for an adiabatic process is^[6]

$p(z)^{\gamma-1}/T(z)^{\gamma}=constant \,$

where $γ$ is the heat capacity ratio ( $γ$ =7/5, for air) and z is the altitude. A second relation between the pressure and temperature is the equation of hydrostatic equilibrium:^[7]

$\frac{dp}{dz} = - \frac {mpg}{RT}$

where g is the standard gravity, R the gas constant, and m the molar mass. Combining these two equations to eliminate the pressure, one arrives at the result for the DALR,^[8]

$-\frac{dT}{dz}= \frac{mg}{R} \frac{\gamma-1}{\gamma}=9.8 \ ^{\circ}\mathrm{C}/\mathrm{km}$ .

Saturated adiabatic lapse rate

When the air is saturated with water vapour (at its dew point), the moist adiabatic lapse rate (MALR) or saturated adiabatic lapse rate (SALR) applies. It varies strongly with the moisture content,^[4] which depends on temperature, and lightly with pressure from +3 °C/km (high temperature near surface) to +9.78 °C/km (very low temperature) as one can see in the diagram. However, at temperatures above freezing it is usually near +4.9 °C/km (+2.7 °F/1000 ft or +1.51°C/1000 ft). The reason for the difference is that latent heat is released when water condenses. Even though there are no more than 10 grams of water in a kilogram of air at 15 degrees Celsius, water's high heat of vaporization creates a significant release of the energy when it condenses (and is an important source of energy in the development of thunderstorms). Until the moisture starts condensing, the parcel of air cools at the DALR so any air that is unsaturated can be assumed to be 'dry'.

Significance in meteorology

The varying environmental lapse rates throughout the earth's atmosphere are of critical importance in meteorology, particularly within the troposphere. They are used to determine if the parcel of rising air will rise high enough for its water to condense to form clouds, and, having formed clouds, whether the air will continue to rise and form bigger shower clouds, and whether these clouds will get even bigger and form cumulonimbus clouds (thunder clouds).

As unsaturated air rises, its temperature drops at the dry adiabatic rate. The dew point also drops, but much more slowly, typically about - 2 °C per 1000 m. If unsaturated air rises far enough, eventually its temperature will reach its dew point, and condensation will begin to form. This altitude is known as the lifting condensation level (LCL) when mechanical lift is present and the convective condensation level (CCL) absent mechanical lift, in which case, the parcel must be heated from below to its convective temperature. The cloud base will be somewhere within the layer bounded by these parameters.

The difference between the dry adiabatic lapse rate and the rate at which the dew point drops is around 8 °C per 1000 m. Given a difference in temperature and dew point readings on the ground, one can easily find the LCL by multiplying the difference by 125 m/°C.

If the environmental lapse rate is less than the moist adiabatic lapse rate, the air is absolutely stable — rising air will cool faster than the surrounding air and lose buoyancy. This often happens in the early morning, when the air near the ground has cooled overnight. Cloud formation in stable air is unlikely.

If the environmental lapse rate is between the moist and dry adiabatic lapse rates, the air is conditionally unstable — an unsaturated parcel of air does not have sufficient buoyancy to rise to the LCL or CCL, and it is stable to weak vertical displacements in either direction. If the parcel is saturated it is unstable and will rise to the LCL or CCL, and either be halted due to an inversion layer of convective inhibition, or if lifting continues, deep, moist convection (DMC) may ensue, as a parcel rises to the level of free convection (LFC), after which it enters the free convective layer (FCL) and usually rises to the equilibrium level (EL).

If the environmental lapse rate is larger than the dry adiabatic lapse rate, it has a superadiabatic lapse rate, the air is absolutely unstable — a parcel of air will gain buoyancy as it rises both below and above the lifting condensation level or convective condensation level. This often happens in the afternoon over many land masses. In these conditions, the likelihood of cumulus clouds, showers or even thunderstorms is increased.

Meteorologists use radiosondes to measure the environmental lapse rate and compare it to the predicted adiabatic lapse rate to forecast the likelihood that air will rise. Charts of the environmental lapse rate are known as thermodynamic diagrams, examples of which being Skew-T log-P diagrams and tephigrams. (See also Thermals).

The difference in moist adiabatic lapse rate and the dry rate is the cause of Föhn winds phenomenon (also known as "Chinook winds" in parts of North America).

Mathematical definition

In general, a lapse rate is expressed as the negative ratio of the temperature change and the altitude change, thus:

$\gamma = -\frac{T_2 - T_1}{z_2 - z_1}$

where $γ$ is the adiabatic lapse rate given in units of temperature divided by units of altitude, T = temperature, and z = altitude, and points 1 and 2 are measurements at two different altitudes.

Note: In some cases, $Γ$ or $α$ can be used to represent the adiabatic lapse rate in order to avoid confusion with other terms symbolized by $γ$ , such as the specific heat ratio^[9] or the psychometric constant^[10].

Additional reading

Beychok, Milton R. (2005). Fundamentals Of Stack Gas Dispersion, Fourth Edition, author-published. ISBN 0-9644588-0-2. www.air-dispersion.com
R. R. Rogers and M. K. Yau (1989). Short Course in Cloud Physics, Third Edition, Butterworth-Heinemann. ISBN 0-7506-3215-1.

References

^ Mark Zachary Jacobson (2005). Fundamentals of Atmospheric Modeling, 2nd Edition, Cambridge University Press. ISBN 0-521-83970-X.
^ C. Donald Ahrens (2006). Meteorology Today, 8th Edition, Brooks/Cole Publishing. ISBN 0-495-01162-2.
^ Todd S. Glickman (June 2000). Glossary of Meteorology, 2nd Edition, American Meteorological Society, Boston. ISBN 1-878220-34-9. (Glossary of Meteorolgy)
^ ^a ^b Adiabatic Lapse Rate, IUPAC Goldbook
^ Danielson, Levin, and Abrams, Meteorology, McGraw Hill, 2003
^ Landau and Lifshitz, Statistical Physics Part 1, Pergamon, 1980
^ Landau and Lifshitz, Fluid Mechanics, Pergamon, 1979
^ Kittel and Kroemer, Thermal Physics, Freeman, 1980; chapter 6, problem 11
^ Salomons, Erik M. (2001). Computational Atmospheric Acoustics, First Edition, Kluwer Academic Publishers. ISBN 1-4020-0390-0.
^ Stull, Roland B. (2001). An Introduction to Boundary Layer Meteorology, First Edition, Kluwer Academic Publishers. ISBN 90-277-2769-4.

Categories: Atmospheric thermodynamics | Fluid mechanics

This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Lapse_rate". A list of authors is available in Wikipedia.
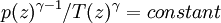
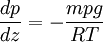
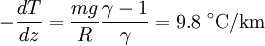