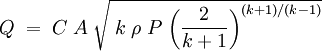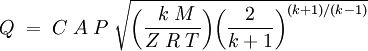Choked flow

Choked flow of a fluid is a fluid dynamic condition caused by the Venturi effect. When a flowing fluid at a certain pressure and temperature flows through a restriction (such as the hole in an orifice plate or a valve in a pipe) into a lower pressure environment, under the conservation of mass the fluid velocity must increase for initially subsonic upstream conditions as it flows through the smaller cross-sectional area of the restriction. At the same time, the Venturi effect causes the pressure to decrease. Choked flow is a limiting condition which occurs when the mass flux will not increase with a further decrease in the downstream pressure environment.

For homogenous fluids, the physical point at which the choking occurs for adiabatic conditions is when the exit plane velocity is at sonic conditions or at a Mach number of 1.^[1][2][3] It is most important to note that the mass flow rate can still be increased by increasing the upstream stagnation pressure.

The choked flow of gases is useful in many engineering applications because the mass flow rate is independent of the downstream pressure, depending only on the temperature and pressure on the upstream side of the restriction. Under choked conditions, valves and calibrated orifice plates can be used to produce a particular mass flow rate.

If the fluid is a liquid, a different type of limiting condition (also known as choked flow) occurs when the Venturi effect acting on the liquid flow through the restriction decreases the liquid pressure to below that of the liquid vapor pressure at the prevailing liquid temperature. At that point, the liquid will partially "boil" into bubbles of vapor and the subsequent collapse of the bubbles causes cavitation. Cavitation is quite noisy and can be sufficiently violent to physically damage valves, pipes and associated equipment. In effect, the vapor bubble formation in the restriction limits the flow from increasing any further.^[4][5]

Additional recommended knowledge

Daily Sensitivity Test

Don't let static charges disrupt your weighing accuracy

What is the Sensitivity of my Balance?

Mass flow rate of a gas at choked conditions

All gases flow from upstream higher stagnation pressure sources to downstream lower pressure sources. There are several situations in which choked flow occurs, such as: change of cross section (as in a convergent-divergent nozzle or flow through an orifice plate), Fanno flow, isothermal flow and Rayleigh flow.

Choking in change of cross section flow

Assuming ideal gas behavior, steady state choked flow occurs when the ratio of the absolute upstream pressure to the absolute downstream pressure is equal to or greater than [ ( k + 1 ) / 2 ] ^{k / ( k - 1 )}, where k is the specific heat ratio of the gas (sometimes called the isentropic expansion factor and sometimes denoted as γ ).

For many gases, k ranges from about 1.09 to about 1.41, and therefore [ ( k + 1 ) / 2 ] ^{k / ( k - 1 )} ranges from 1.7 to about 1.9 ... which means that choked flow usually occurs when the absolute source vessel pressure is at least 1.7 to 1.9 times as high as the absolute downstream pressure.

When the gas velocity is choked, the equation for the mass flow rate in SI metric units is: ^[1][2][3][6]

where the terms are defined in the table below. If the density ρ is not known directly, then it is useful to eliminate it using the Ideal gas law corrected for the real gas compressibility:

so that the mass flow rate is primarily dependent on the cross-sectional area A of the hole and the supply pressure P, and only weakly dependent on the temperature T. The rate does not depend on the downstream pressure at all. All other terms are constants that depend only on the composition of the material in the flow.

The above equations calculate the steady state mass flow rate for the stagnation pressure and temperature existing in the upstream pressure source.

If the gas is being released from a closed high-pressure vessel, the above steady state equations may be used to approximate the initial mass flow rate. Subsequently, the mass flow rate will decrease during the discharge as the source vessel empties and the pressure in the vessel decreases. Calculating the flow rate versus time since the initiation of the discharge is much more complicated, but more accurate. Two equivalent methods for performing such calculations are explained and compared online.^[7]

The technical literature can be very confusing because many authors fail to explain whether they are using the universal gas law constant R which applies to any ideal gas or whether they are using the gas law constant R_s which only applies to a specific individual gas. The relationship between the two constants is R_s = R / M.

Notes:

• The above equations are for a real gas.
• For a monatomic ideal gas, Z = 1 and ρ is the ideal gas density.
• kmole = 1000 moles = 1000 gram-moles = kilogram-mole

Thin-plate orifices

The flow of real gases through thin-plate orifices never becomes fully choked. The mass flow rate through the orifice continues to increase as the downstream pressure is lowered to a perfect vacuum, though the mass flow rate increases slowly as the downstream pressure is reduced below the critical pressure.^[8] "Cunningham (1951) first drew attention to the fact that choked flow will not occur across a standard, thin, square-edged orifice."^[9]

Minimum pressure ratio required for choked flow to occur

The minimum pressure ratios required for choked conditions to occur (when some typical industrial gases are flowing) are presented in Table 1. The ratios were obtained using the criteria that choked flow occurs when the ratio of the absolute upstream pressure to the absolute downstream pressure is equal to or greater than [ ( k + 1 ) / 2 ] ^{k / ( k - 1 )} , where k is the specific heat ratio of the gas.

Notes:

• P_u = absolute upstream gas pressure
• P_d = absolute downstream gas pressure
• k values obtained from:
  1. Perry, Robert H. and Green, Don W. (1984). Perry's Chemical Engineers' Handbook, 6th Edition, McGraw-Hill Company. ISBN 0-07-049479-7. 
  2. Phillips Petroleum Company (1962). Reference Data For Hydrocarbons And Petro-Sulfur Compounds, Second Printing, Phillips Petroleum Company. 

See also

• Accidental release source terms includes mass flow rate equations for non-choked gas flows as well.
• Orifice plate includes derivation of non-choked gas flow equation.
• Laval nozzles are Venturi tubes that produce supersonic gas velocities as the tube and the gas are first constricted and then the tube and gas are expanded beyond the choke plane.
• Rocket engine nozzles discusses how to calculate the exit velocity from nozzles used in rocket engines.

References