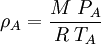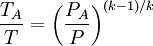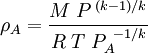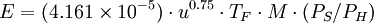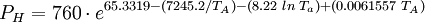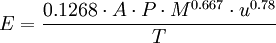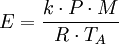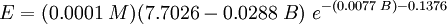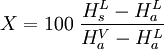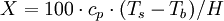To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Accidental release source termsAccidental release source terms are the mathematical equations that quantify the flow rate at which accidental releases of air pollutants into the ambient environment can occur at industrial facilities such as petroleum refineries, petrochemical plants, natural gas processing plants, oil and gas transportation pipelines, chemical plants, and many other industrial activities. Governmental regulations in a good many countries require that the probability of such accidental releases be analyzed and their quantitative impact upon the environment and human health be determined so that mitigating steps can be planned and implemented. There are a number of mathematical calculation methods for determining the flow rate at which gaseous and liquid pollutants might be released from various types of accidents. Such calculational methods are referred to as source terms, and this article on accidental release source terms explains some of the calculation methods used for determining the mass flow rate at which gaseous pollutants may be accidentally released. Product highlight
Accidental release of pressurized gasWhen gas stored under pressure in a closed vessel is discharged to the atmosphere through a hole or other opening, the gas velocity through that opening may be choked (i.e., it has attained a maximum) or it may be non-choked. Choked velocity, also referred to as sonic velocity, occurs when the ratio of the absolute source pressure to the absolute downstream pressure is equal to or greater than [(k + 1) ÷ 2 ] k÷(k - 1 ), where k is the specific heat ratio of the discharged gas (sometimes called the isentropic expansion factor and sometimes denoted as γ). For many gases, k ranges from about 1.09 to about 1.41, and therefore [(k + 1) ÷ 2 ] k÷(k - 1 ) ranges from 1.7 to about 1.9, which means that choked velocity usually occurs when the absolute source vessel pressure is at least 1.7 to 1.9 times as high as the absolute downstream ambient atmospheric pressure. When the gas velocity is choked, the equation for the mass flow rate in SI metric units is:[1][2][3][4]
or this equivalent form:
For the above equations, it is important to note that although the gas velocity reaches a maximum and becomes choked, the mass flow rate is not choked. The mass flow rate can still be increased if the source pressure is increased. Whenever the ratio of the absolute source pressure to the absolute downstream ambient pressure is less than
[ ( k + 1 ) ÷ 2 ] k ÷ ( k - 1 ), then the gas velocity is non-choked (i.e., sub-sonic) and the equation for mass flow rate is:
or this equivalent form:
The above equations calculate the initial instantaneous mass flow rate for the pressure and temperature existing in the source vessel when a release first occurs. The initial instantaneous flow rate from a leak in a pressurized gas system or vessel is much higher than the average flow rate during the overall release period because the pressure and flow rate decrease with time as the system or vessel empties. Calculating the flow rate versus time since the initiation of the leak is much more complicated, but more accurate. Two equivalent methods for performing such calculations are presented and compared at www.air-dispersion.com/feature2.html. The technical literature can be very confusing because many authors fail to explain whether they are using the universal gas law constant R which applies to any ideal gas or whether they are using the gas law constant Rs which only applies to a specific individual gas. The relationship between the two constants is Rs = R/M. Notes:
Ramskill's equation for non-choked mass flowP.K. Ramskill's equation [5][6] for the non-choked flow of an ideal gas is shown below as equation (1): (1) The gas density, ρA, in Ramskill's equation is the ideal gas density at the downstream conditions of temperature and pressure and it is defined in equation (2) using the ideal gas law: (2) Since the downstream temperature TA is not known, the isentropic expansion equation below [7] is used to determine TA in terms of the known upstream temperature T: (3) Combining equations (2) and (3) results in equation (4) which defines ρA in terms of the known upstream temperature T: (4) Using equation (4) with Ramskill's equation (1) to determine non-choked mass flow rates for ideal gases gives identical results to the results obtained using the non-choked flow equation presented in the previous section above. Evaporation of non-boiling liquid poolThree different methods of calculating the rate of evaporation from a non-boiling liquid pool are presented in this section. The results obtained by the three methods are somewhat different. The U.S. Air Force methodThe following equations are for predicting the rate at which liquid evaporates from the surface of a pool of liquid which is at or near the ambient temperature. The equations were derived from field tests performed by the U.S. Air Force with pools of liquid hydrazine. [2]
If TP = 0 °C or less, then TF = 1.0
The U.S. EPA methodThe following equations are for predicting the rate at which liquid evaporates from the surface of a pool of liquid which is at or near the ambient temperature. The equations were developed by the United States Environmental Protection Agency using units which were a mixture of metric usage and United States usage.[3] The non-metric units have been converted to metric units for this presentation.
The U.S. EPA also defined the pool depth as 0.01 m (i.e., 1 cm) so that the surface area of the pool liquid could be calculated as:
Notes:
Stiver and Mackay's methodThe following equations are for predicting the rate at which liquid evaporates from the surface of a pool of liquid which is at or near the ambient temperature. The equations were developed by Warren Stiver and Dennis Mackay of the Chemical Engineering Department at the University of Toronto. [8]
Evaporation of boiling cold liquid poolThe following equation is for predicting the rate at which liquid evaporates from the surface of a pool of cold liquid (i.e., at a liquid temperature of about 0 °C or less). [2]
Adiabatic flash of liquified gas releaseLiquified gases such as ammonia or chlorine are often stored in cylinders or vessels at ambient temperatures and pressures well above atmospheric pressure. When such a liquified gas is released into the ambient atmosphere, the resultant reduction of pressure causes some of the liquified gas to vaporize immediately. This is known as "adiabatic flashing" and the following equation, derived from a simple heat balance, is used to predict how much of the liquified gas is vaporized.
If the enthalpy data required for the above equation is unavailable, then the following equation may be used.
See alsoReferences
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Accidental_release_source_terms". A list of authors is available in Wikipedia. |





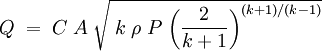
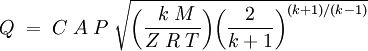
![Q\;=\;C\;A\;\sqrt{\;2\;\rho\;P\;\bigg(\frac{k}{k-1}\bigg)\Bigg[\,\bigg(\frac{\;P_A}{P}\bigg)^{2/k}-\;\,\bigg(\frac{\;P_A}{P}\bigg)^{(k+1)/k}\;\Bigg]}](images/math/6/9/f/69f05b512cda9244d65bef6827c3f27c.png)
![Q\;=\;C\;A\;P\;\sqrt{\bigg(\frac{2\;M}{Z\;R\;T}\bigg)\bigg(\frac{k}{k-1}\bigg)\Bigg[\,\bigg(\frac{\;P_A}{P}\bigg)^{2/k}-\;\,\bigg(\frac{\;P_A}{P}\bigg)^{(k+1)/k}\;\Bigg]}](images/math/9/1/e/91e73ec82a65f3f70f74bf1a52510c20.png)
![Q = C \;\rho_A\;A\;\sqrt{\frac{\;\,2\;P}{\rho}\cdot\frac{k}{k-1}\cdot{\Bigg[\; 1 - {\bigg(\frac{P_A}{P}\bigg)^{(k-1)/k)}}\Bigg]}}](images/math/5/d/8/5d879e8f38c5845dfbba1ca79113fa51.png)