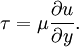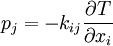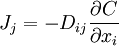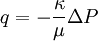To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Constitutive equationIn structural analysis, constitutive relations connect applied stresses or forces to strains or deformations. The constitutive relations for linear materials are linear, and termed Hooke's law. Product highlightMore generally, in physics, a constitutive equation is a relation between two physical quantities (often tensors) that is specific to a material or substance, and does not follow directly from physical law. It is combined with other equations that do represent physical laws to solve some physical problem, like the flow of a fluid in a pipe, or the response of a crystal to an electric field. The first constitutive equation (constitutive law) was discovered by Hooke and is known as Hooke's law. It deals with the case of linear elastic materials. But the expression constitutive law was first used in the doctoral thesis of Walter Noll on 1954 whose advisor was Clifford Truesdell at Indiana University. Actually the concept of constitutive law was introduced by Walter Noll which now has found very wide acceptance. Walter Noll's thesis is now quoted in the Oxford English Dictionary. Some constitutive equations are simply phenomenological; others are derived from first principles. A constitutive equation frequently has a parameter taken to be a constant of proportionality in ideal systems. Examples
or and in tensor form, or, equivalently,
See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Constitutive_equation". A list of authors is available in Wikipedia. |





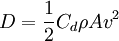
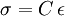
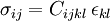
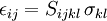
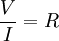 or
or