To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Direct numerical simulationA direct numerical simulation (DNS) is a simulation in computational fluid dynamics in which the Navier-Stokes equations are numerically solved without any turbulence model. This means that the whole range of spatial and temporal scales of the turbulence must be resolved. All the spatial scales of the turbulence must be resolved in the computational mesh, from the smallest dissipative scales (Kolmogorov microscales), up to the integral scale L, associated with the motions containing most of the kinetic energy. The Kolmogorov scale,η, is given by Product highlight
where ν is the kinematic viscosity and ε is the rate of kinetic energy dissipation. On the other hand, the integral scale depends usually on the spatial scale of the boundary conditions. To satisfy these resolution requirements, the number N of points along a given mesh direction with increments h, must be
so that the integral scale is contained within the computational domain, and also
so that the Kolmogorov scale can be resolved. Since
where u' is the root mean square (RMS) of the velocity, the previous relations imply that a three-dimensional DNS requires a number of mesh points N3 satisfying
where Re is the turbulent Reynolds number
Hence, the memory storage requirement in a DNS grows very fast with the Reynolds number. In addition, given the very large memory necessary, the integration of the solution in time must be done by an explicit method. This means that in order to be accurate, the integration must be done with a time step, Δt, small enough such that a fluid particle moves only a fraction of the mesh spacing h in each step. That is,
(C is here the Courant number). The total time interval simulated is generally proportional to the turbulence time scale τ given by
Combining these relations, and the fact that h must be of the order of η, the number of time-integration steps must be proportional to L / (Cη). By other hand, from the definitions for Re, η and L given above, it follows that
and consequently, the number of time steps grows also as a power law of the Reynolds number. One can estimate that the number of floating-point operations required to complete the simulation is proportional to the number of mesh points and the number of time steps, and in conclusion, the number of operations grows as Re3. Therefore, the computational cost of DNS is very high, even at low Reynolds numbers. For the Reynolds numbers encountered in most industrial applications, the computational resources required by a DNS would exceed the capacity of the most powerful computers currently available. However, direct numerical simulation is a useful tool in fundamental research in turbulence. Using DNS it is possible to perform "numerical experiments", and extract from them information difficult or impossible to obtain in the laboratory, allowing a better understanding of the physics of turbulence. Also, direct numerical simulations are useful in the development of turbulence models for practical applications, such as sub-grid scale models for Large eddy simulation (LES) and models for methods that solve the Reynolds-averaged Navier-Stokes equations (RANS). This is done by means of "a priori" tests, in which the input data for the model is taken from a DNS simulation, or by "a posteriori" tests, in which the results produced by the model are compared with those obtained by DNS. The biggest DNS in the world, up to this date, used 40963 mesh points. It was carried out in the Japanese Earth Simulator supercomputer in 2002. See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Direct_numerical_simulation". A list of authors is available in Wikipedia. |





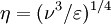
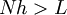 ,
,
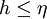 ,
,
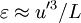 ,
,
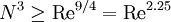
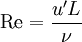 .
.
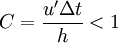
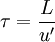 .
.
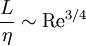 ,
,


