To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Molecular symmetryMolecular symmetry in chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as many of a molecule's chemical properties, such as its dipole moment and its allowed spectroscopic transitions (based on selection rules such as the Laporte rule) can be predicted or explained based on the molecule's symmetry. Virtually every university level textbook on physical chemistry, quantum chemistry, and inorganic chemistry devotes a chapter to symmetry.[1][2][3][4][5] While various frameworks for the study of molecular symmetry exist, group theory is the predominant one. This framework is also useful in studying the symmetry of molecular orbitals, with applications such as the Hückel method, ligand field theory, and the Woodward-Hoffmann rules. Another framework on a larger scale is the use of crystal systems to describe crystallographic symmetry in bulk materials. Many techniques exist for the practical assessment of molecular symmetry, including X-ray crystallography and various forms of spectroscopy. Spectroscopic notation is based on symmetry considerations. Product highlight
Symmetry conceptsThe study of symmetry in molecules is an adaptation of mathematical group theory. ElementsThe symmetry of a molecule can be described by 5 types of symmetry elements.
OperationsThe 5 symmetry elements have associated with them 5 symmetry operations. They are often, although not always, distinguished from the respective elements by a caret. Thus Ĉn is the rotation of a molecule around an axis and Ê is the identity operation. A symmetry element can have more than one symmetry operation associated with it. Since C1 is equivalent to E, S1 to σ and S2 to i, all symmetry operations can be classified as either proper or improper rotations. Point groupsA point group is a set of symmetry operations forming a mathematical group, for which at least one point remains fixed under all operations of the group. In three dimensions there are 32 such point groups, 30 of which are relevant to chemistry. Their classification is based on the Schoenflies notation. Group theoryA set of symmetry operations form a group, with operator the application of the operations itself, when:
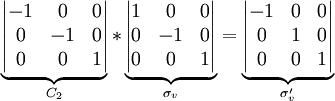
The order of a group is the number of symmetry operations for that group. For example, the point group for the water molecule is C2v, with symmetry operations E, C2, σv and σv'. Its order is thus 4. Each operation is its own inverse. As an example of closure, a C2 rotation followed by a σv reflection is seen to be a σv' symmetry operation:
Common point groupsThe following table contains a list of point groups with representative molecules.
RepresentationsThe symmetry operations can be represented in many ways. A convenient representation is by matrices. For any vector representing a point in Cartesian coordinates, left-multiplying it gives the new location of the point transformed by the symmetry operation. Composition of operations corresponds to matrix multiplication: in the C2v example this is: Although an infinite number of such representations exist, the irreducible representations (or "irreps") of the group are commonly used, as all other representations of the group can be described as a linear combination of the irreducible representations. Character tablesFor each point group, a character table summarizes information on its symmetry operations and on its irreducible representations. As there are always equal numbers of irreducible representations and classes of symmetry operations, the tables are square. The table itself consists of characters which represent how a particular irreducible representation transforms when a particular symmetry operation is applied. Any symmetry operation in a molecule's point group acting on the molecule itself will leave it unchanged. But for acting on a general entity, such as a vector or an orbital, this need not be the case. The vector could change sign or direction, and the orbital could change type. For simple point groups, the values are either 1 or −1: 1 means that the sign or phase (of the vector or orbital) is unchanged by the symmetry operation (symmetric) and −1 denotes a sign change (asymmetric). The representations are labeled according to a set of conventions:
The tables also captures information about how the Cartesian basis vectors, rotations about them, and quadratic functions of them transform by the symmetry operations of the group, by noting which irreducible representation transforms in the same way. These indications are conventionally on the right hand side of the tables. This information is useful because chemically important orbitals (in particular p and d orbitals) have the same symmetries as these entities. The character table for the C2v symmetry point group is given below:
Continuing the C2v example, consider the oxygen atomic orbitals in water: the 2px is oriented perpendicular to the plane of the molecule and switches sign with a C2 and a σv'(yz) operation, but remains unchanged with the other two operations (obviously, the character for the identity operation is always +1). This orbital's character set is thus {1, −1, 1, −1}, corresponding to the B1 irreducible representation. Similarly, the 2pz orbital is seen to have the symmetry of the A1 irreducible representation, 2py B2, and the 3dxy orbital A2. These assignments and others are noted in the rightmost two columns of the table. Historical backgroundHans Bethe used characters of point group operations in his study of ligand field theory in 1929, and Eugene Wigner used group theory to explain molecular vibrations. The first character tables were compiled by László Tisza (1933), again in connection to vibrational spectra. Robert Mulliken was the first to publish character tables in English (1933), and E. Bright Wilson used them in 1934 to predict the symmetry of vibrational normal modes.[6] The complete set of 32 point groups was published in 1936 by Rosenthal and Murphy.[7] References
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Molecular_symmetry". A list of authors is available in Wikipedia. |





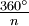 results in a molecule indistinguishable from the original. This is also called an n-fold rotational axis and abbreviated Cn. Examples are the C2 in water and the C3 in
results in a molecule indistinguishable from the original. This is also called an n-fold rotational axis and abbreviated Cn. Examples are the C2 in water and the C3 in