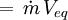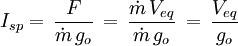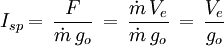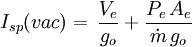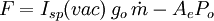To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rocket engine nozzle
The main type of rocket engine nozzles used in modern rocket engines is the de Laval nozzle which is used to expand and accelerate the combustion gases, from burning propellants, so that the exhaust gases exiting the nozzles are at hypersonic velocities. Product highlight
HistoryThe de Laval nozzle was first used in an early rocket engine developed by Robert Goddard, one of the fathers of modern rocketry. Subsequently, Walter Thiel's implementation of it made possible Germany's use of the V2 rocket to bomb England during World War II. Atmospheric useThe optimal size of a rocket engine nozzle to be used within the atmosphere is when the exit pressure equals ambient pressure, which decreases with altitude. For rockets travelling from the Earth to orbit, a simple nozzle design is only optimal at one altitude, losing efficiency and wasting fuel at other altitudes. If the pressure of the jet leaving the nozzle is above ambient pressure then a nozzle is said to be 'underexpanded'; if the jet is below ambient pressure then it 'overexpanded'. Slight overexpansion causes a slight reduction in efficiency, but otherwise does little harm. However, if the jet pressure is approximately 2.5 times lower than ambient then 'flow separation' occurs. This can cause jet instabilities that can cause damage to the nozzle or simply cause control difficulties of the vehicle or the engine. In some cases it is desirable for reliability and safety reasons to ignite a rocket engine on the ground that will be used all the way to orbit. In most cases the optimal pressure is ambient, however if most of the thrust comes from (ambient pressure) boosters at takeoff, then the trades push to using an overexpanded nozzle. This is the technique used on the Space shuttle's main engines. Vacuum useFor nozzles that are used in vacuum or at very high altitude, it is impossible to match ambient pressure and rather larger area ratio nozzles are usually more efficient. However, a very long nozzle has significant mass and a length that optimises overall vehicle performance can always be found. Additionally, as the temperature of the gas in the nozzle decreases some components of the exhaust gases (such as water vapour from the combustion process) may liquefy or even freeze. This is highly undesirable and needs to be avoided. Magnetic nozzles have been proposed for some types of propulsion (for example VASIMR), in which the flow of plasma or ions are directed by magnetic fields instead of walls made of solid materials. These can be advantageous since a magnetic field itself cannot melt and the plasma can be at millions of kelvins. But there are often thermal problems in the coils, particularly if superconducting coils are used to form the throat and expansion fields. 1-D Analysis of gas flow in rocket engine nozzlesThe analysis of gas flow through de Laval nozzles involves a number of concepts and assumptions:
As the combustion gas enters the rocket nozzle, it is travelling at subsonic velocities. As the throat contracts down the gas is forced to accelerate until at the nozzle throat, where the cross-sectional area is the smallest, the linear velocity becomes sonic. From the throat the cross-sectional area then increases, the gas expands and the linear velocity becomes progressively more supersonic. The linear velocity of the exiting exhaust gases can be calculated using the following equation [1][2][3]
Some typical values of the exhaust gas velocity Ve for rocket engines burning various propellants are:
As a note of interest, Ve is sometimes referred to as the ideal exhaust gas velocity because it based on the assumption that the exhaust gas behaves as an ideal gas. As an example calculation using the above equation, assume that the propellant combustion gases are: at an absolute pressure entering the nozzle of P = 7.0 MPa and exit the rocket exhaust at an absolute pressure of Pe = 0.1 MPa; at an absolute temperature of T = 3500 K; with an isentropic expansion factor of k = 1.22 and a molar mass of M = 22 kg/kmol. Using those values in the above equation yields an exhaust velocity Ve = 2802 m/s or 2.80 km/s which is consistent with above typical values. The technical literature can be very confusing because many authors fail to explain whether they are using the universal gas law constant R which applies to any ideal gas or whether they are using the gas law constant Rs which only applies to a specific individual gas. The relationship between the two constants is Rs = R/M. Specific ImpulseThrust is the force which moves a rocket through the air, and through space. Thrust is generated by the propulsion system of the rocket through the application of Newton's third law of motion: "For every action there is an equal and opposite reaction". A gas or working fluid is accelerated out the rear of the rocket engine nozzle and the rocket is accelerated in the opposite direction. The thrust of a rocket engine nozzle can be defined as:[1][2][4][5]
The specific impulse, Isp, is the ratio of the amount of thrust produced to the weight flow of the propellants. It is a measure of the fuel efficiency of a rocket engine. It can be obtained from:[6]
In certain cases, where Pe equals Po, then: In cases where this may not be the case since for a rocket nozzle Pe is proportional to and hence: which is simply the vacuum thrust minus the force of the ambient atmospheric pressure acting over the exit plane. Essentially then, for rocket nozzles, the ambient pressure acting over the engine largely cancels but effectively acts over the exit plane of the rocket engine in a rearward direction, while the exhaust jet generates forward thrust.
Aerodynamic back-pressure and optimum expansionAs the gas travels down the expansion part of the nozzle the pressure and temperature decreases and the speed of the gas increases. The supersonic nature of the exhaust jet means that the pressure of the exhaust can be significantly different to ambient pressure- the outside air is unable to equalize the pressure upstream due to the very high jet velocity. Therefore, for supersonic nozzles, it is actually possible for the pressure of the gas exiting the nozzle to go significantly below or very greatly above ambient pressure. If the exit pressure is too low, then the jet can separate from the nozzle. This is often unstable and the jet will generally cause large off-axis thrusts, and may mechanically damage the nozzle. This separation generally occurs if the exit pressure goes below roughly 30-45% of ambient, but may be delayed to far lower pressures if the nozzle is designed to increase the pressure at the rim, as is achieved with the SSME (1-2 psi at 15 psi ambient).[8] In addition, as the rocket engine starts up or throttles, the chamber pressure varies and this generates different levels of efficiency. At low chamber pressures the engine is almost inevitably going to be grossly over-expanded. Optimum shapeThe ratio of the area of the narrowest part of the nozzle to the exit plane area is mainly what determines how efficiently the expansion of the exhaust gases is converted into linear velocity; the exhaust velocity and therefore the thrust of the rocket engine, although the gas properties have an effect as well. The shape of the nozzle also modestly affects how efficiently the expansion of the exhaust gases is converted into linear motion. The simplest nozzle shape is a ~12 degree internal angle cone, which is about 97% efficient. Smaller angles give very slightly higher efficiency, larger angles give lower efficiency. More complex shapes of revolution are frequently used, such as Bell nozzles or parabolic shapes. This gives perhaps 1% higher efficiency than the cone nozzle, and is shorter and lighter. These shapes are widely used on launch vehicles and other rockets where weight is at a premium. They are of course, harder to fabricate, so are typically more costly. There is also a theoretical optimum nozzle shape for maximum exhaust speed, however, a shorter, suboptimal bell shape is typically used due to its much lower weight, shorter length, lower drag losses, and only very marginally lower exhaust speed.[8] Advanced designsA number of more sophisticated designs have been proposed, such as the plug nozzle, expanding nozzle, Stepped nozzles and the aerospike nozzle each of which adapt in some way to changing ambient pressure. There is also a SERN (Single Expansion Ramp Nozzle), a linear expansion nozzle where the gas pressure transfers work only on one side and which could be described as a single-sided aerospike nozzle. See also
References
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rocket_engine_nozzle". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





![V_e = \sqrt{\;\frac{T\;R}{M}\cdot\frac{2\;k}{k-1}\cdot\bigg[ 1-(P_e/P)^{(k-1)/k}\bigg]}](images/math/7/c/f/7cfc8d726613be693b94f69352a4ee55.png)
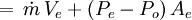
![=\,\dot{m}\,\bigg[V_e + \bigg(\frac{P_e - P_o}{\dot{m}}\bigg)A_e\bigg]](images/math/5/0/b/50bca8a0f560ed1134bdbb98d1c4fcde.png)