To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Van der Waals equationThe van der Waals equation is an equation of state for a fluid composed of particles that have a non-zero size and a pairwise attractive inter-particle force (such as the van der Waals force.) It was derived by Johannes Diderik van der Waals in 1873, based on a modification of the ideal gas law. The equation approximates the behavior of real fluids, taking into account the nonzero size of molecules and the attraction between them. Additional recommended knowledge
EquationThe first form of the van der Waals equation is where
Upon introduction of Avogadro's constant NA, the number of moles n, and the total number of particles nNA, the equation can be cast into the second (better known) form
where
A careful distinction must be drawn between the volume available to a particle and the volume of a particle. In particular, in the first equation ValidityAbove the critical temperature the van der Waals equation is an improvement of the ideal gas law, and for lower temperatures the equation is also qualitatively reasonable for the liquid state and the low-pressure gaseous state. However, the van der Waals model cannot be taken seriously in a quantitative sense, it is only useful for qualitative purposes.[1] In the first-order phase transition range of (p,V,T) (where the liquid phase and the gas phase are in equilibrium) it does not exhibit the empirical fact that p is constant as a function of V for a given temperature. DerivationIn the usual textbooks one finds two different derivations. One is the conventional derivation that goes back to van der Waals and the other is a statistical mechanics derivation. The latter has its major advantage that it makes explicit the intermolecular potential, which is out of sight in the first derivation.
Next, we introduce a pairwise attractive force between the particles. Van der Waals assumed that, notwithstanding the existence of this force, the density of the fluid is homogeneous. Further he assumed that the range of the attractive force is so small that the great majority of the particles do not feel that the container is of finite size. That is, the bulk of the particles do not notice that they have more attracting particles to their right than to their left when they are relatively close to the left-hand wall of the container. The same statement holds with left and right interchanged. Given the homogeneity of the fluid, the bulk of the particles do not experience a net force pulling them to the right or to the left. This is different for the particles in surface layers directly adjacent to the walls. They feel a net force from the bulk particles pulling them into the container, because this force is not compensated by particles on the side where the wall is (another assumption here is that there is no interaction between walls and particles). This net force decreases the force exerted onto the wall by the particles in the surface layer. The net force on a surface particle, pulling it into the container, is proportional to the number density C = NA / Vm. The number of particles in the surface layers is, again by assuming homogeneity, also proportional to the density. In total, the force on the walls is decreased by a factor proportional to the square of the density and the pressure (force per unit surface) is decreased by
so that Upon writing n for the number of moles and nVm = V, the equation obtains the second form given above, It is of some historical interest to point out that van der Waals in his Nobel prize lecture gave credit to Laplace for the argument that pressure is reduced proportional to the square of the density.
Conventional derivationConsider first one mole of gas which is composed of non-interacting point particles that satisfy the ideal gas law Next assume that all particles are hard spheres of the same finite radius r (the van der Waals radius). The effect of the finite volume of the particles is to decrease the available void space in which the particles are free to move. We must replace V by V-b, where b is called the excluded volume. The corrected equation becomes The excluded formula is not just equal to the volume occupied by the solid, finite size, particles, but actually four times that volume. To see this we must realize that a particle is surrounded by a sphere of radius r' = 2r (two times the original radius) that is forbidden for the centers of the other particles. If the distance between two particle centers would be smaller than 2r, it would mean that the two particles penetrate each other, which, by definition, hard spheres are unable to do. Statistical thermodynamics derivationThe canonical partition function Q of an ideal gas consisting of N = nNA identical particles, is where Λ is the thermal de Broglie wavelength, with the usual definitions: h is Planck's constant, m the mass of a particle, k Boltzmann's constant and T the absolute temperature. In an ideal gas r is the distance between the centers of the spheres and d is the distance where the hard spheres touch each other (twice the van der Waals radius). The depth of the van der Waals well is ε. Because the particles are independent the total partition function still factorizes, Q = qN / N!, but the intermolecular potential necessitates two modifications to The total attraction felt by a single particle is, where we assumed that in a shell of thickness dr there are N/V 4π r²dr particles. Performing the integral we get Hence, we obtain by the use of Stirling's approximation, It is convenient to take T out of Λ and to rewrite this expression as where Φ is a constant. From statistical thermodynamics we know that
so that Other thermodynamic parametersWe reiterate that the extensive volume V is related to the volume per particle v=V/N where N = nNA is the number of particles in the system. The equation of state does not give us all the thermodynamic parameters of the system. We can take the equation for the Helmholtz energy A From the equation derived above for lnQ, we find This equation expresses A in terms of its natural variables V and T , and therefore gives us all thermodynamic information about the system. The mechanical equation of state was already derived above The entropy equation of state yields the entropy (S ) from which we can calculate the internal energy Similar equations can be written for the other thermodynamic potentials and the chemical potential, but expressing any potential as a function of pressure p will require the solution of a third-order polynomial, which yields a complicated expression. Therefore, expressing the enthalpy and the Gibbs energy as functions of their natural variables will be complicated. Reduced formAlthough the material constants a and b in the usual form of the van der Waals equation differs for every single fluid considered, the equation can be recast into an invariant form applicable to all fluids. Defining the following reduced variables (
where The first form of the van der Waals equation of state given above can be recast in the following reduced form: This equation is invariant (i.e., the same equation of state, viz., above, applies) for all fluids. Thus, when measured in intervals of the critical values of various quantities, all fluids obey the same equation of state -- the reduced van der Waals equation of state. This is also known as the Principle of corresponding states. In the sense that we have eliminated the appearance of the individual material constants a and b in the equation, this can be considered unity in diversity.
Application to compressible fluidsThe equation is also usable as a PVT equation for compressible fluids (e.g. polymers). In this case specific volume changes are small and it can be written in a simplified form:
where
Maxwell Equal Area RuleBelow the critical temperature (T’<1) an isotherm of the Van der Waals equation oscillates as shown. Along the red portion of the isotherm
See also
References
Categories: Gases | Gas laws | Fluid dynamics | Chemical engineering |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Van_der_Waals_equation". A list of authors is available in Wikipedia. |





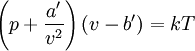
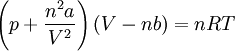 ,
,
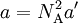
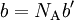
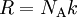
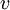 refers to the empty space available per particle. That is,
refers to the empty space available per particle. That is, 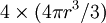 , which is four times the proper volume of the particle. It was a point of concern to van der Waals that the factor four yields actually an upper bound, empirical values for
, which is four times the proper volume of the particle. It was a point of concern to van der Waals that the factor four yields actually an upper bound, empirical values for  ,
,
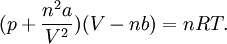
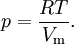
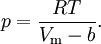
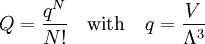
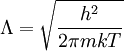
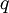 is the partition function of a single particle in a container of volume V. In order to derive the van der Waals equation we assume now that each particle moves independently in an average potential field offered by the other particles. The averaging over the particles is easy because we will assume that the particle density of the van der Waals fluid is homogeneous.
The interaction between a pair of particles, which are hard spheres, is taken to be
is the partition function of a single particle in a container of volume V. In order to derive the van der Waals equation we assume now that each particle moves independently in an average potential field offered by the other particles. The averaging over the particles is easy because we will assume that the particle density of the van der Waals fluid is homogeneous.
The interaction between a pair of particles, which are hard spheres, is taken to be
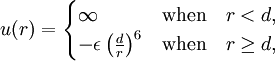
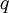 . First, because of the finite size of the particles, not all of V is available, but only
. First, because of the finite size of the particles, not all of V is available, but only 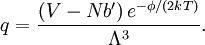
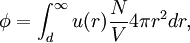
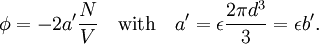
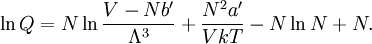
![\ln Q = N\left(1+\ln\Bigg[ \frac{ (V-Nb')\,T^{3/2}}{N\Phi}\Bigg]\right) + \frac{N^2 a'}{V kT} ,](images/math/d/0/8/d08cfdb8a74b800308aa7c3df686873c.png)
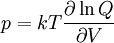 ,
,
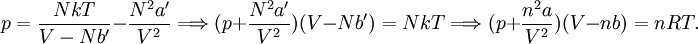
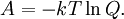
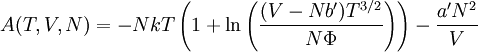
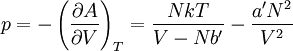
![S = -\left(\frac{\partial A}{\partial T}\right)_V =Nk\left[ \ln\left(\frac{(V-Nb')T^{3/2}}{N\Phi}\right)+\frac{5}{2} \right]](images/math/8/3/9/83993c81b88a8e3cc0d0776909e4fa53.png)
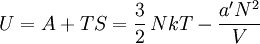
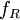 ,
, 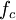 is the reduced and
is the reduced and 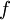 , respectively),
, respectively),
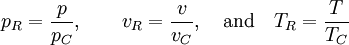 ,
,
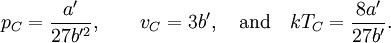
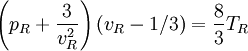
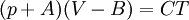 ,
,
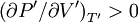 which is unstable; the Van der Waals equation fails to describe real substances in this region. To fix this problem James Clerk Maxwell (1875) replaces the isotherm between a-c with a horizontal line positioned so that the areas of the two hatched regions are equal. The flat line portion of the isotherm now corresponds to liquid-vapor equilibrium. The portions a-d and c-e are interpreted as metastable states of super-heated liquid and super-cooled vapor respectively.
which is unstable; the Van der Waals equation fails to describe real substances in this region. To fix this problem James Clerk Maxwell (1875) replaces the isotherm between a-c with a horizontal line positioned so that the areas of the two hatched regions are equal. The flat line portion of the isotherm now corresponds to liquid-vapor equilibrium. The portions a-d and c-e are interpreted as metastable states of super-heated liquid and super-cooled vapor respectively. 
