To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Davydov soliton
Product highlightDavydov soliton is a quantum quasiparticle representing a propagating along the protein α-helix self-trapped amide I excitation that is a solution of the Davydov Hamiltonian. The Davydov model describes the interaction of the amide I vibrations with the hydrogen bonds that stabilize the α-helix of proteins. The elementary excitations within the α-helix are given by the phonons which correspond to the deformational oscillations of the lattice, and the excitons which describe the internal amide I excitations of the peptide groups. Referring to the atomic structure of an α-helix region of protein the mechanism that creates the Davydov soliton (polaron, exciton) can be described as follows: vibrational energy of the C=O stretching (or amide I) oscillators that is localized on the α-helix acts through a phonon coupling effect to distort the structure of the α-helix, while the helical distortion reacts again through phonon coupling to trap the amide I oscillation energy and prevent its dispersion. This effect is called self-localization or self-trapping. [1][2][3] Solitons in which the energy is distributed in a fashion preserving the helical symmetry are dynamically unstable, and such symmetrical solitons once formed decay rapidly when they propagate. On the other hand, an asymmetric soliton which spontaneously breaks the local translational and helical symmetries possesses the lowest energy and is a robust localized entity. [4] Davydov's Hamiltonian is formally similar to the Fröhlich-Holstein Hamiltonian for the interaction of electrons with a polarizable lattice. Thus the Hamiltonian of the energy operator
where The quasiparticle (exciton) Hamiltonian
where the index The phonon Hamiltonian
Finally, the interaction Hamiltonian
The mathematical techniques that are used to analyze Davydov's soliton are similar to some that have been developed in polaron theory. In this context the Davydov's soliton corresponds to a polaron that is (i) large so the continuum limit approximation in justified, (ii) acoustic because the self-localization arises from interactions with acoustic modes of the lattice, and (iii) weakly coupled because the anharmonic energy is small compared with the phonon bandwidth [5]. The Davydov soliton is a quantum quasiparticle and it obeys Heisenberg's uncertainty principle. Thus any model that does not impose translational invariance is flawed by construction [5]. Supposing that the Davydov soliton is localized to 5 turns of the α-helix results in significant uncertainty in the velocity of the soliton Δv = 133 m/s, a fact that is obscured if one models the Davydov soliton as a classical object. There are three possible fundamental approaches towards Davydov model: [6][8] (i) the quantum theory, in which both the amide I vibration (excitons) and the lattice site motion (phonons) are treated quantum mechanically; (ii) the mixed quantum-classical theory, in which the amide I vibration is treated quantum mechanically but the lattice is classical; and (iii) the classical theory, in which both the amide I and the lattice motions are treated classically. References
|
||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Davydov_soliton". A list of authors is available in Wikipedia. | ||||||||||||





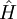 is
is
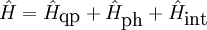
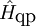 is the
is the 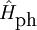 is the
is the 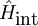 is the
is the 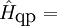
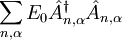
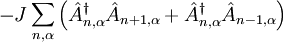
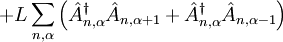
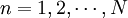 counts the peptide groups along the α-helix spine, the index
counts the peptide groups along the α-helix spine, the index 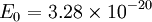 J is the energy of the amide I
vibration (CO stretching),
J is the energy of the amide I
vibration (CO stretching), 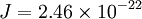 J is the
J is the 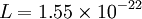 J is the
dipole-dipole coupling energy between a particular amide I bond and those on adjacent spines in the same unit cell of the
J is the
dipole-dipole coupling energy between a particular amide I bond and those on adjacent spines in the same unit cell of the 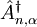 and
and 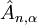 are respectively
the
are respectively
the ![\hat{H}_{\textrm{ph}}=\frac{1}{2}\sum_{n,\alpha}\left[w(\hat{u}_{n+1,\alpha}-\hat{u}_{n,\alpha})^{2}+\frac{\hat{p}_{n,\alpha}^{2}}{M}\right]](images/math/8/4/7/84799bb9a90eb2411a9ab4957c3d1567.png)
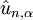 is the displacement operator from the equilibrium position of the
is the displacement operator from the equilibrium position of the 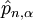 is the momentum operator of the
is the momentum operator of the ![\hat{H}_{\textrm{int}}=\chi\sum_{n,\alpha}\left[(\hat{u}_{n+1,\alpha}-\hat{u}_{n,\alpha})\hat{A}_{n,\alpha}^{\dagger}\hat{A}_{n,\alpha}\right]](images/math/d/9/2/d924ce2a1b5d5828f188bf8b19398091.png)


