To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
QuarkoniumIn particle physics, quarkonium (pl. quarkonia) designates a flavorless meson whose constituents are a quark and its own antiquark. Examples of quarkonia are the J/ψ (which is a charmonium, or charm quark/anti-charm quark state) and the Υ (a bottomonium, or bottom quark/anti-bottom quark state). Because of the high mass of the top quark, a toponium does not exist, since the quark decays through the electroweak interaction before a bound state can form. Usually quarkonium refers only to charmonium and bottomonium, and not to any of the lighter quark/anti-quark states. This usage is because the lighter quarks (up, down, and strange) have very similar masses, compared to the heavier quarks, and so the physical states actually seen in experiments are quantum mechanical mixtures of the light quark states. The much larger mass differences between the charm and bottom quarks and the lighter quarks, results in states that are well defined in terms of a quark/anti-quark pair of a given flavor. Product highlight
Charmonium statesIn the following table, the same particle can be named with the spectroscopic notation or with its mass. In some cases excitation series are used: Ψ' is the first excitation of Ψ (for historical reasons, this one is called J/ψ particle); Ψ" is a second excitation, and so on. That is, names in the same cell are synonymous. Some of the states are predicted, but have not been identified; others are unconfirmed. Particle X(3872) quantum numbers are unknown; its identity is debated. It may be:
In 2005, the BaBar experiment announced the discovery of a new state: Y(4260). (See article, arXiv:hep-ex/0506081.) CLEO and Belle have since corroborated these observations. At first, Y(4260) was thought to be a charmonium state, but the evidence suggests more exotic explanations, such as a D "molecule", a 4-quark construct, or a hybrid meson.
Notes:
Bottomonium statesIn the following table, the same particle can be named with the spectroscopic notation or with its mass. Some of the states are predicted, but have not been identified; others are unconfirmed.
Notes:
QCD and quarkoniaThe computation of the properties of mesons in Quantum chromodynamics (QCD) is a fully non-perturbative one. As a result, the only general method available is a direct computation using lattice QCD (LQCD) techniques. However, other techniques are effective for heavy quarkonia as well. The light quarks in a meson move at relativistic speeds, since the mass of the bound state is much larger than the mass of the quark. However, the speed of the charm and the bottom quarks in their respective quarkonia is sufficiently smaller, so that relativistic effects affect these states much less. It is estimated that the speed, v, is roughly 0.3 times the speed of light for charmonia and roughly 0.1 times the speed of light for bottomonia. The computation can then be approximated by an expansion in powers of v/c and v2/c2. This technique is called non-relativistic QCD (NRQCD). NRQCD has also been quantized as a lattice gauge theory, which provides another technique for LQCD calculations to use. Good agreement with the bottomonium masses has been found, and this provides one of the best non-perturbative tests of LQCD. For charmonium masses the agreement is not as good, but the LQCD community is actively working on improving their techniques. Work is also being done on calculations of such properties as widths of quarkonia states and transition rates between the states. An early, but still effective, technique uses models of the effective potential to calculate masses of quarkonia states. In this technique, one uses the fact that the motion of the quarks that comprise the quarkonium state is non-relativistic to assume that they move in a static potential, much like non-relativistic models of the hydrogen atom. One of the most popular potential models is the so-called Cornell potential where r is the effective radius of the quarkonium state a and b are parameters. This potential has two parts. The first part, a / r corresponds to the potential induced by one-gluon exchange between the quark and its anti-quark, and is known as the Coulombic part of the potential, since its 1 / r form is identical to the well-known Coulombic potential induced by the electromagnetic force. The second part, br, is known as the confinement part of the potential, and parameterizes the poorly-understood non-perturbative effects of QCD. Generally, when using this approach, a convenient form for the wave function of the quarks is taken, and then a and b are determined by fitting the results of the calculations to the masses of well-measured quarkonium states. Relativistic and other effects can be incorporated into this approach by adding extra terms to the potential, much in the same way that they are for the hydrogen atom in non-relativistic quantum mechanics. This approach has no good theoretical motivation, but is popular because it allows for accurate predictions of quarkonia parameters without a lengthy lattice computation, and provides a separation between the short-distance Coulombic effects and the long-distance confinement effects that can be useful in understanding the quark/anti-quark force generated by QCD. Disappearance of quarkonia has been suggested as a diagnostic of the formation of the quark-gluon plasma in experiments. See also
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Quarkonium". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





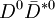 molecule.
molecule.