To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
LeptonIn physics, a lepton is a particle with spin -1/2 that does not experience the strong interaction (that is, the strong nuclear force). The leptons form a family of fermions that are distinct from the other known family of fermions, the quarks. Product highlight
Properties of leptonsThere are three known flavors of lepton: the electron, the muon, and the tau. Each flavor is represented by a pair of particles called a weak doublet. One is a massive charged particle that bears the same name as its flavor (like the electron). The other is a nearly massless neutral particle called a neutrino (such as the electron neutrino). All six of these particles have corresponding antiparticles (such as the positron or the electron antineutrino). All known charged leptons have a single unit of negative or positive electric charge (depending on whether they are particles or antiparticles) and all of the neutrinos and antineutrinos have zero electric charge. The charged leptons have two possible spin states, while only one helicity is observed for the neutrinos (all the neutrinos are left-handed, and all the antineutrinos are right-handed). The masses of the leptons also obey a simple relation, known as the Koide formula, but at present this relationship cannot be explained. When particles interact, generally the number of leptons of the same type (electrons and electron neutrinos, muons and muon neutrinos, tau leptons and tau neutrinos) remains the same. This principle is known as conservation of lepton number. Conservation of the number of leptons of different flavors (for example, electron number or muon number) may sometimes be violated (as in neutrino oscillation). A much stronger conservation law is the total number of leptons of all flavors, which is violated by a tiny amount in the Standard Model by the so-called chiral anomaly. The couplings of the leptons to gauge bosons are flavor-independent. This property is called lepton universality and has been tested in measurements of the tau and muon lifetimes and of Z-boson partial decay widths, particularly at the SLC and LEP experiments. Table of the leptons
Note that the neutrino masses are known to be non-zero because of neutrino oscillation, but their masses are sufficiently light that they have not been measured directly as of 2007. However there have been measured (indirectly based on the oscillation periods) the differences of the mass squares between the neutrinos, which have been estimated
The names "mu" and "tau" seem to have been selected due to their places in the Greek alphabet; mu is seven letters after epsilon (electron), whereas tau is seven letters after mu. EtymologyAccording to the Oxford English Dictionary, the name "lepton" (from Greek leptos) was first used by physicist Léon Rosenfeld in 1948:
The name originates from before the discovery in the 1970s of the heavy tau lepton, which is nearly twice the mass of a proton. See alsoIn Popular Culture
References
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Lepton". A list of authors is available in Wikipedia. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





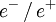
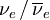
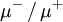
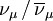
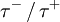
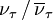
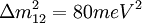 and
and 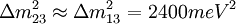 . This leads to the following conclusions:
. This leads to the following conclusions:


