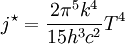To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stefan–Boltzmann lawThe Stefan–Boltzmann law, also known as Stefan's law, states that the total energy radiated per unit surface area of a black body in unit time (known variously as the black-body irradiance, energy flux density, radiant flux, or the emissive power), j*, is directly proportional to the fourth power of the black body's thermodynamic temperature T (also called absolute temperature): A more general case is of a gray body, the one that doesn't absorb or emit the full amount of radiative flux. Instead, it radiates a portion of it, characterized by its emissivity, ε: The irradiance j* has dimensions of power density (energy per time per square distance), and the SI units of measure are joules per second per square meter, or equivalently, watts per square meter. The SI unit for absolute temperature T is the kelvin. ε is the emissivity of the gray body; if it is a perfect blackbody, ε = 1. Still in more general (and realistic) case, the emissivity depends on the wavelength, ε = ε(λ). The constant of proportionality σ, called the Stefan–Boltzmann constant or Stefan's constant, is non-fundamental in the sense that it derives from other known constants of nature. The value of the constant is where k is the Boltzmann constant, h is Planck's constant, and c is the speed of light in a vacuum. Thus at 100 K the energy flux density is 5.67 W/m2, at 1000 K 56,700 W/m2, etc. The Stefan–Boltzmann law is an example of a power law. The law was discovered experimentally by Jožef Stefan (1835-1893) in 1879 and derived theoretically, using thermodynamics, by Ludwig Boltzmann (1844-1906) in 1884. Boltzmann treated a certain ideal heat engine with the light as a working matter instead of the gas. This law is the only physical law of nature named after a Slovene physicist. The law is valid only for ideal black objects, the perfect radiators, called black bodies. Stefan published this law on March 20 in the article Über die Beziehung zwischen der Wärmestrahlung und der Temperatur (On the relationship between thermal radiation and temperature) in the Bulletins from the sessions of the Vienna Academy of Sciences. Product highlight
Derivation of the Stefan–Boltzmann lawIntegration of intensity derivationThe law can be derived by considering a small flat black body surface radiating out into a half-sphere. This derivation uses spherical coordinates, with φ as the zenith angle and θ as the azimuthal angle; and the small flat blackbody surface lies on the xy-plane, where φ = π/2. The intensity of the blackbody surface is given by Planck's law as: To restate the meaning of I: the quantity The integral with respect to θ can be done immediately; it's just 2π. The integral with respect to φ can also be done by observing that sin(φ)cos(φ) = 0.5 sin(2φ); it yields 1/2. The remainder requires a u-substitution given by ν = u k T / h, dν = du k T / h. Substituting throughout gives: The integral on the right can be done in a number of ways (one is included in this article's appendix) -- its answer is π4/15, giving the result that, for a perfect blackbody surface: Finally, this proof started out only considering a small flat surface. However, any differentiable surface can be approximated by a bunch of small flat surfaces. So long as the geometry of the surface does not cause the blackbody to reabsorb its own radiation, the total energy radiated is just the sum of the energies radiated by each surface; and the total surface area is just the sum of the areas of each surface -- so this law holds for all convex blackbodies, too, so long as the surface has the same temperature throughout. Thermodynamic derivationThe fact that the energy density of the box containing radiation is proportional to T4 can be derived using thermodynamics. It follows from classical electrodynamics that the radiation pressure P is related to the internal energy density: The total internal energy of the box containing radiation can thus be written as: Inserting this in the fundamental law of thermodynamics yields the equation: We can now use this equation to derive a Maxwell relation. From the above equation it can be seen that: and The symmetry of second derivatives of S w.r.t. P and V then implies: Because the pressure is proportional to the internal energy density it depends only on the temperature and not on the volume. In the derivative on the r.h.s. the temperature is thus a constant. Evaluating the derivatives gives the differential equation: This implies that ExamplesTemperature of the SunWith his law Stefan also determined the temperature of the Sun's surface. He learned from the data of Charles Soret (1854–1904) that the energy flux density from the Sun is 29 times greater than the energy flux density of a warmed metal lamella. A round lamella was placed at such a distance from the measuring device that it would be seen at the same angle as the Sun. Soret estimated the temperature of the lamella to be approximately 1900 °C to 2000 °C. Stefan surmised that ⅓ of the energy flux from the Sun is absorbed by the Earth's atmosphere, so he took for the correct Sun's energy flux a value 3/2 times greater, namely 29 × 3/2 = 43.5. Precise measurements of atmospheric absorption were not made until 1888 and 1904. The temperature Stefan obtained was a median value of previous ones, 1950 °C and the absolute thermodynamic one 2200 K. As 2.574 = 43.5, it follows from the law that the temperature of the Sun is 2.57 times greater than the temperature of a lamella, so Stefan got a value of 5430 °C or 5700 K (modern value is 5780 K). This was the first sensible value for the temperature of the Sun. Before this, values ranging from as low as 1800 °C to as high as 13,000,000 °C were claimed. The lower value of 1800 °C was determined by Claude Servais Mathias Pouillet (1790-1868) in 1838 using the Dulong-Petit law. Pouilett also took just half the value of the Sun's correct energy flux. Perhaps this result reminded Stefan that the Dulong-Petit law could break down at large temperatures. Temperature of starsThe temperature of stars other than the Sun can be approximated using a similar means by treating the emitted energy as a black body radiation.[1][2] So: where L is the luminosity, σ is the Stefan–Boltzmann constant, R is the stellar radius and T is the effective temperature. This same formula can be used to compute the approximate radius of a main sequence star relative to the sun: where With the Stefan–Boltzmann law, astronomers can easily infer the radii of stars. The law is also met in the thermodynamics of black holes in so called Hawking radiation. Effective temperature of the EarthSimilarly we can calculate the effective temperature of the Earth TE by equating the energy received from the Sun and the energy transmitted by the Earth:
where TS is the temperature of the Sun, rS the radius of the Sun, and a0 is the distance between the Earth and the Sun. Thus resulting in an effective temperature of 6°C on the surface of the Earth. In summary, the surface of the Sun is 21 times as hot as that of the Earth taken as a blackbody, and therefore it emits 190,000 times as much energy per square meter. The distance from the Sun to the Earth is 215 times the radius of the Sun, reducing the energy per square meter by a factor 46,000. Taking into account that the cross-section of a sphere is one fourth of its surface area, we see that there is equilibrium of approximately 342 W per m2 surface area, or 1,370 W per m2 cross-sectional area. The above derivation is a rough approximation only as it assumes the Earth is a perfect blackbody. If we include the effect of Terrestrial albedo which is about 30% (meaning the actual amount of solar energy absorbed by our planet is 70% of top of atmosphere irradiation), the above equation gives an average Earth surface temperature of 255 K only. The "missing" 33 K between such calculated value and the actual measured one (288 K) is deemed to be the result of greenhouse gases, namely water vapor, carbon dioxide and methane [3]. However such a reasoning has to be taken very carefully as the Stefan–Boltzmann law is not directly applicable to non-blackbody objects; variation in albedo (absorptivity or emissivity) as a function of wavelength, for example as due to greenhouse gases, can change the resulting equilibrium temperature substantially. AppendixIn one of the above derivations, the following integral appeared: There are a number of ways to do this integration; a simple one is given in the appendix of the Planck's law article. This appendix does the integral by contour integration. Consider the function: Using the Taylor expansion of the sine function, it should be evident that the coefficient of the k3 term would be exactly -J/6. By expanding both sides in powers of k, we see that J is minus 6 times the coefficient of k3 of the series expansion of f(k). So, if we can find a closed form for f(k), its Taylor expansion will give J. In turn, sin(x) is the imaginary part of eix, so we can restate this as: To evaluate the integral in this equation we consider the contour integral: where C(ε,R) is the contour from ε to R, then to R + 2πi, then to ε + 2πi, then we go to the point 2πi − εi, avoiding the pole at 2πi by taking a clockwise quarter circle with radius ε and center 2πi. From there we go to εi, and finally we return to ε, avoiding the pole at zero by taking a clockwise quarter circle with radius ε and center zero. Because there are no poles in the integration contour we have: We now take the limit The left hand side is the sum of the integral from ε to R and from R + 2πi to 2πi + ε. We can rewrite the integrand of the integral on the r.h.s. as follows: If we now take the imaginary part of both sides of Eq. (1) and take the limit after using the relation:
Using that the series expansion of coth(x) is given by: we see that the coefficient of k3 of the series expansion of f(k) is follows. See also
References
|
|||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stefan–Boltzmann_law". A list of authors is available in Wikipedia. |


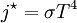
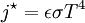
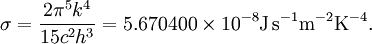



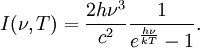
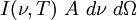 is the power radiated by a surface of area A through a solid angle dΩ in the frequency range (ν, ν+dν). To derive the Stefan–Boltzmann law, we must integrate Ω over the half-sphere and integrate ν from 0 to ∞. Furthermore, because of
is the power radiated by a surface of area A through a solid angle dΩ in the frequency range (ν, ν+dν). To derive the Stefan–Boltzmann law, we must integrate Ω over the half-sphere and integrate ν from 0 to ∞. Furthermore, because of 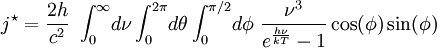
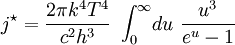
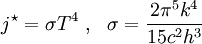
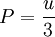
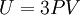
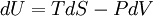
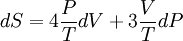
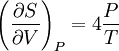
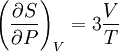
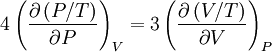
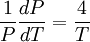
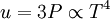
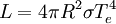
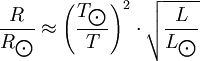
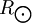 , is the solar radius, and so forth.
, is the solar radius, and so forth.
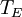
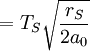
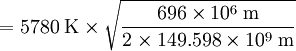
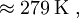
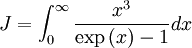
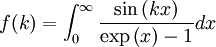
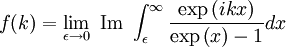
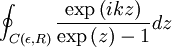
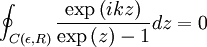
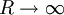 . In this limit the contribution from the segment from
. In this limit the contribution from the segment from 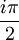 times the residues at the poles we find:
times the residues at the poles we find:
![\left[1-\exp\left(-2\pi k\right) \right]\int_{\epsilon}^{\infty}\frac{\exp\left(ikx\right)}{\exp\left(x\right)-1} dx= i \int_{\epsilon}^{2\pi-\epsilon}\frac{\exp\left(-ky\right)}{\exp\left(iy\right)-1}dy+i\frac{\pi}{2}\left[1+\exp\left(-2\pi k\right)\right]\mbox{ (1)}](images/math/8/6/3/8635c8a99783117f73d89c71b1317123.png)
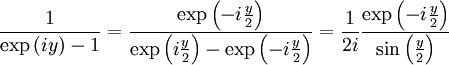
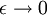 we find:
we find:
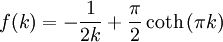
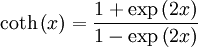 .
.
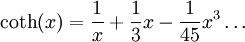
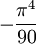 . This then implies that
. This then implies that 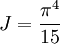 and the result
and the result