Supercomputer and quantum simulations solve a difficult problem of materials science
Researchers from Japan successfully estimate the bending energy of disiloxane molecule with ultra-fine molecular simulations run on a supercomputer
Understanding the structural properties of molecules found in nature or synthesized in the laboratory has always been the bread and butter of materials scientists. But, with advancements in science and technology, the endeavor has become even more ambitious: discovering new materials with highly desirable properties. To accomplish such a feat systematically, materials scientists rely upon sophisticated simulation techniques that incorporate the rules of quantum mechanics, the same rules which govern the molecules themselves.
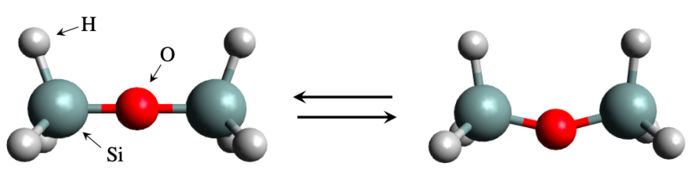
Disiloxane molecule structure in linear form (left) and bent form (right). A global team of scientists considered the bending energy of a silicate molecule, disiloxane. Although the system appears to be simple and tractable, the bending energy calculation is actually a difficult problem to solve by the conventional simulation methods.
Dr. Kenta Hongo from JAIST
The simulation-based approach has been remarkably successful, so much so that an entire field of study called materials informatics has been dedicated to it. But there have also been instances of failure. A notable example comes from disiloxane, a silicon (Si)-containing compound consisting of a Si-O-Si bridge with three hydrogen atoms at each end. The structure is simple enough, and yet it has been notoriously difficult to estimate just how much energy is needed to bend the Si-O-Si bridge. Experimental results have been inconsistent and theoretical calculations have yielded widely different values due to the sensitivity of the calculated properties to parameter choices and level of theory.
Fortunately, an international research team led by Dr. Kenta Hongo, Associate Professor at Japan Advanced Institute of Science and Technology, has now managed to solve this problem. In their study published in Physical Chemistry Chemical Physics, the team achieved this feat by using a state-of-the-art simulation technique called “first-principles quantum Monte Carlo method” that finally overcame the difficulties other standard techniques could not surmount.
But does it all just boil down to better simulations? Not quite. “Getting an answer that does not agree with the experimentally known value is, in itself, not surprising. The agreement can improve with more careful, and more expensive, simulations. But with disiloxane, the agreement actually becomes worse with more careful simulations,” explains Dr. Hongo. “What our method has achieved, rather, is good results without much dependence on the adjustment parameters, so that we don’t need to worry about whether the adjusted values are sufficient.”
The team compared the first-principles quantum Monte Carlo approach with other standard techniques, such as “density functional theory” (DFT) calculations and “coupled cluster method with single and double substitutions and noniterative triples” (CCSD(T)), along with empirical measurements from previous studies. The three methods differed mainly in their sensitivity towards the “completeness” of basis sets (a set of functions used to define the quantum wavefunctions).
It turned out that for DFT and CCSD(T), the choice of basis set affected the amplitude as well as positions of zero amplitude for the wavefunctions, while for quantum Monte Carlo, it only affected the zero amplitude positions. This allowed one to tweak the amplitude such that the wavefunction shape approached that of an exact solution. “This self-healing property of the amplitude works well to reduce the basis-set dependence and lower the bias arising from an incomplete basis set in calculating the bending energy barrier,” elaborates Dr. Hongo.
While this is an exciting development in itself, Prof. Hongo points out the bigger picture. “Molecular simulations are widely used to design new medicines and catalysts. Getting rid of the fundamental difficulties in using them greatly contributes to the design of such materials. With our powerful supercomputers, the method used in our study could be a standard strategy for overcoming such difficulties,” he says.
This is indeed deserving of being called a “quantum leap”!
Original publication
Other news from the department science
Most read news
More news from our other portals
Last viewed contents
Intricate processes in photosynthesis decoded using advanced electron microscopy technique - This enables breakthroughs in multiple areas of biological and chemical research
Tip tricks control reactions in a single molecule - Pulses from an atom-sharp tip enable researchers to break and form chemical bonds at will
Accessible_surface_area
Flip-flop_kinetics
Reverse_vending_machine
Asbestos_Project_Monitor
Table_of_medication_secernated_in_kidney
Tuneable Catalysis: Solving the Particle Size Puzzle - Scientists succeed in linking microscopic and macroscopic approaches - and thus solve an old puzzle
