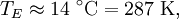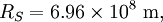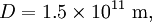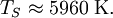To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Black body
In physics, a black body is an object that absorbs all electromagnetic radiation that falls onto it. No radiation passes through it and none is reflected. It is this lack of both transmission and reflection to which the name refers. These properties make black bodies ideal sources of thermal radiation. A blackbody is an abstract concept. It entails a system in which the thermal energy is carried via electromagnetic radiation. With this it is possible to approximate the temperature of the object through the wavelength of the light that is emitted. Black bodies above this temperature however, produce radiation at visible wavelengths starting at red, going through orange, yellow, and white before ending up at blue as the temperature increases. The term "black body" was introduced by Gustav Kirchhoff in 1860. The light emitted by a black body is called black-body radiation (or cavity radiation), and has a special place in the history of quantum mechanics.[1] Additional recommended knowledge
ExplanationIn the laboratory, black-body radiation is approximated by the radiation from a small hole entrance to a large cavity, a hohlraum. Any light entering the hole would have to reflect off the walls of the cavity multiple times before it escaped, in which process it is nearly certain to be absorbed. This occurs regardless of the wavelength of the radiation entering (as long as it is small compared to the hole). The hole, then, is a close approximation of a theoretical black body and, if the cavity is heated, the spectrum of the hole's radiation (i.e., the amount of light emitted from the hole at each wavelength) will be continuous, and will not depend on the material in the cavity (compare with emission spectrum). By a theorem proved by Kirchhoff, this curve depends only on the temperature of the cavity walls.[2] Calculating this curve was a major challenge in theoretical physics during the late nineteenth century. The problem was finally solved in 1901 by Max Planck as Planck's law of black-body radiation.[3] By making changes to Wien's Radiation Law (not to be confused with Wien's displacement law) consistent with Thermodynamics and Electromagnetism, he found a mathematical formula fitting the experimental data in a satisfactory way. To find a physical interpretation for this formula, Planck had then to assume that the energy of the oscillators in the cavity was quantized (i.e., integer multiples of some quantity). Einstein built on this idea and proposed the quantization of electromagnetic radiation itself in 1905 to explain the photoelectric effect. These theoretical advances eventually resulted in the superseding of classical electromagnetism by quantum electrodynamics. Today, these quanta are called photons and the black-body cavity may be thought of as containing a gas of photons. In addition, it led to the development of quantum versions of statistical mechanics, called Fermi-Dirac statistics and Bose-Einstein statistics, each applicable to a different class of particles. See also fermion and boson.
The wavelength at which the radiation is strongest is given by Wien's displacement law, and the overall power emitted per unit area is given by the Stefan-Boltzmann law. So, as temperature increases, the glow color changes from red to yellow to white to blue. Even as the peak wavelength moves into the ultra-violet enough radiation continues to be emitted in the blue wavelengths that the body will continue to appear blue. It will never become invisible — indeed, the radiation of visible light increases monotonically with temperature.[4] The radiance or observed intensity is not a function of direction. Therefore a black body is a perfect Lambertian radiator. Real objects never behave as full-ideal black bodies, and instead the emitted radiation at a given frequency is a fraction of what the ideal emission would be. The emissivity of a material specifies how well a real body radiates energy as compared with a black body. This emissivity depends on factors such as temperature, emission angle, and wavelength. However, it is typical in engineering to assume that a surface's spectral emissivity and absorptivity do not depend on wavelength, so that the emissivity is a constant. This is known as the grey body assumption. Although Planck's formula predicts that a black body will radiate energy at all frequencies, the formula is only applicable when many photons are being measured. For example, a black body at room temperature (300 K) with one square meter of surface area will emit a photon in the visible range once every thousand years or so, meaning that for most practical purposes, the black body does not emit in the visible range. When dealing with non-black surfaces, the deviations from ideal black-body behavior are determined by both the geometrical structure and the chemical composition, and follow Kirchhoff's Law: emissivity equals absorptivity, so that an object that does not absorb all incident light will also emit less radiation than an ideal black body.
In astronomy, objects such as stars are frequently regarded as black bodies, though this is often a poor approximation. An almost perfect black-body spectrum is exhibited by the cosmic microwave background radiation. Hawking radiation is black-body radiation emitted by black holes. Equations governing black bodiesPlanck's law of black-body radiationwhere
Wien's displacement lawThe relationship between the temperature T of a black body, and wavelength λmax at which the intensity of the radiation it produces is at a maximum is The nanometer is a convenient unit of measure for optical wavelengths. Note that 1 nanometer is equivalent to 10−9 meters. Stefan–Boltzmann lawThe total energy radiated per unit area per unit time Radiation emitted by a human body
Black-body laws can be applied to human beings. For example, some of a person's energy is radiated away in the form of electromagnetic radiation, most of which is infrared. The net power radiated is the difference between the power emitted and the power absorbed:
Applying the Stefan-Boltzmann law,
The total surface area of an adult is about 2 m², and the mid- and far-infrared emissivity of skin and most clothing is near unity, as it is for most nonmetallic surfaces.[5][6] Skin temperature is about 33°C,[7] but clothing reduces the surface temperature to about 28°C when the ambient temperature is 20°C.[8] Hence, the net radiative heat loss is about
The total energy radiated in one day is about 9 MJ (million joules), or 2000 kcal (food calories). Basal metabolic rate for a 40-year-old male is about 35 kcal/(m²·h),[9] which is equivalent to 1700 kcal per day assuming the same 2 m² area. However, the mean metabolic rate of sedentary adults is about 50% to 70% greater than their basal rate.[10] There are other important thermal loss mechanisms, including convection and evaporation. Conduction is negligible since the Nusselt number is much greater than unity. Evaporation (perspiration) is only required if radiation and convection are insufficient to maintain a steady state temperature. Free convection rates are comparable, albeit somewhat lower, than radiative rates.[11] Thus, radiation accounts for about 2/3 of thermal energy loss in cool, still air. Given the approximate nature of many of the assumptions, this can only be taken as a crude estimate. Ambient air motion, causing forced convection, or evaporation reduces the relative importance of radiation as a thermal loss mechanism. Also, applying Wien's Law to humans, one finds that the peak wavelength of light emitted by a person is
This is why thermal imaging devices designed for human subjects are most sensitive to 7–14 micrometers wavelength. Temperature relation between a planet and its starHere is an application of black-body laws. It is a rough derivation that gives an order of magnitude answer. See p. 380-382 of Planetary Science, for further discussion.[12] FactorsThe surface temperature of a planet depends on a few factors:
For the inner planets, incident and emitted radiation have the most significant impact on surface temperature. This derivation is concerned mainly with that. AssumptionsIf we assume the following:
then we can derive a formula for the relationship between the Earth's surface temperature and the Sun's surface temperature. DerivationTo begin, we use the Stefan-Boltzmann law to find the total power (energy/second) the Sun is emitting:
The Sun emits that power equally in all directions. Because of this, the Earth is hit with only a tiny fraction of it. This is the power from the Sun that the Earth absorbs:
Even though the earth only absorbs as a circular area πR2, it emits equally in all directions as a sphere:
Now, in the first assumption the earth is in thermal equilibrium, so the power absorbed must equal the power emitted:
Many factors cancel from both sides and this equation can be greatly simplified. The resultAfter canceling of factors, the final result is
In other words, the temperature of the Earth depends only on the surface temperature of the Sun, the radius of the Sun, and the distance between the Earth and the Sun. Temperature of the SunIf we substitute in the measured values for Earth, we'll find the effective temperature of the Sun to be This is within three percent of the standard measure of 5780 kelvins which makes the formula valid for most scientific and engineering applications. See also
References
Other textbooks
Categories: Thermodynamics | Electromagnetic radiation |
||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Black_body". A list of authors is available in Wikipedia. |





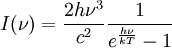
 is the amount of energy per unit surface area per unit time per unit solid angle emitted in the frequency range between ν and ν+dν;
is the amount of energy per unit surface area per unit time per unit solid angle emitted in the frequency range between ν and ν+dν;
 is the
is the  is Planck's constant;
is Planck's constant;
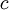 is the
is the 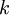 is
is 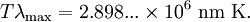
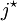 (in
(in 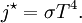
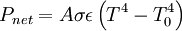 .
.
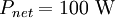 .
.
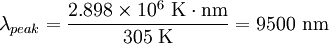 .
.
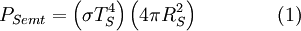
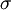 is the
is the 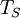 is the surface temperature of the Sun, and
is the surface temperature of the Sun, and
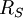 is the radius of the Sun.
is the radius of the Sun.
 is the radius of the Earth and
is the radius of the Earth and
 is the distance between the Sun and the Earth.
is the distance between the Sun and the Earth.
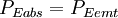
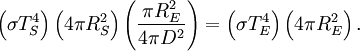
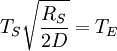
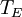 is the average surface temperature of the Earth.
is the average surface temperature of the Earth.