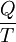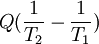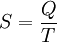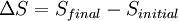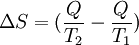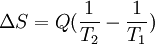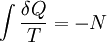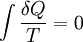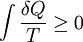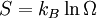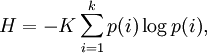History of entropy

The history of entropy, essentially, is the development of ideas set forth to theoretically understand why a certain amount of functionable energy released from combustion reactions is always lost to dissipation or friction, i.e. unusable. In this direction, in 1698 engineer Thomas Savery built the first engine. Soon others followed, as the Newcomen engine [1712] and the Cugnot steam tricycle [1769]. These early engines, however, were inefficient converting less than two percent of the input energy into useful work output. Essentially, a great deal of useful energy was dissipated or lost into what seemed like a state of immeasurable randomness. Over the next two centuries, physicists began to pry away at this puzzle of lost energy; the result was the concept of entropy.

In the early 1850s, Rudolf Clausius began to put the concept of "energy turned to waste" on a differential footing. Essentially, he set forth the concept of the thermodynamic system and positioned the argument that in any irreversible process a small amount of heat energy δQ is incrementally dissipated across the system boundary.

Specifically, in 1850 Clausius published his first memoir in which he presented a verbal argument as to why Carnot’s theorem, proposing the equivalence of heat and work, i.e. Q = W, was not perfectly correct and as such it would need amendment. In 1854, Clausius states: "In my memoir 'On the Moving Force of Heat, &c.', I have shown that the theorem of the equivalence of heat and work, and Carnot’s theorem, are not mutually exclusive, by that, by a small modification of the latter, which does not affect its principle, they can be brought into accordance." This small modification on the latter is what developed into the second law of thermodynamics.

Additional recommended knowledge

Weighing the right way

Essential Laboratory Skills Guide

How to quickly check pipettes?

Historical definitions

1854 definition

In his 1854 memoir, Clausius first develops the concepts of interior work, i.e. "those which the atoms of the body exert upon each other", and exterior work, i.e. "those which arise from foreign influences which the body may be exposed", which may act on a working body of fluid or gas, typically functioning to work a piston. He then discusses the three types of heat by which Q may be divided:

1. Heat employed in increasing the heat actually existing in the body.
2. Heat employed in producing the interior work.
3. Heat employed in producing the exterior work.

Building on this logic, and following a mathematical presentation of the first fundamental theorem, Clausius then presents us with the first-ever mathematical formulation of entropy, although at this point in the development of his theories calls it "equivalence-value", most likely so to have relation to the mechanical equivalent of heat which was developing at the time. He states:^[1]

the second fundamental theorem in the mechanical theory of heat may thus be enunciated:

If two transformations which, without necessitating any other permanent change, can mutually replace one another, be called equivalent, then the generations of the quantity of heat Q from work at the temperature t , has the equivalence-value:

and the passage of the quantity of heat Q from the temperature T₁ to the temperature T₂, has the equivalence-value:

wherein T is a function of the temperature, independent of the nature of the process by which the transformation is effected.

This is the first-ever mathematical formulation of entropy; at this point, however, Clausius had not yet affixed the concept with the label entropy as we currently know it; this would come in the following several years.^[2] In modern terminology, we think of this equivalence-value as "entropy", symbolized by S. Thus, using the above description, we can calculate the entropy change ΔS for the passage of the quantity of heat Q from the temperature T₁, through the "working body" of fluid (see heat engine), which was typically a body of steam, to the temperature T₂ as shown below:   If we make the assignment:

Then, the entropy change or "equivalence-value" for this transformation is:

which equals:

and by factoring out Q, we have the following form, as was derived by Clausius:

1856 definition

In 1856, Clausius stated what he called the "second fundamental theorem in the mechanical theory of heat" in the following form:

where N is the "equivalence-value" of all uncompensated transformations involved in a cyclical process. This equivalence-value was a precursory formulation of entropy.^[3]

1862 definition

Main article: disgregation

In 1862, Clausius stated what he calls the “theorem respecting the equivalence-values of the transformations” or what is now known as the second law of thermodynamics, as such:

The algebraic sum of all the transformations occurring in a cyclical process can only be positive, or, as an extreme case, equal to nothing.

Quantitatively, Clausius states the mathematical expression for this theorem is as follows. Let δQ be an element of the heat given up by the body to any reservoir of heat during its own changes, heat which it may absorb from a reservoir being here reckoned as negative, and T the absolute temperature of the body at the moment of giving up this heat, then the equation:

must be true for every reversible cyclical process, and the relation:

must hold good for every cyclical process which is in any way possible. This was an early formulation of the second law and one of the original forms of the concept of entropy.

1865 definition

In 1865, Clausius gave irreversible heat loss, or what he had previously been calling "equivalence-value", a name:^[4][5]

Although Clausius did not specify why he choose the symbol "S" to represent entropy, it is arguable that Clausius choose "S" in honor of S. Carnot, i.e. Sadi Carnot, to whose 1824 article Clausius devoted over 15 years worth of work and research on.^[6] From the first page of his original 1850 article "On the Motive Power of Heat, and on the Laws which can be Deduced from it for the Theory of Heat", Clausius calls "S. Carnot" the most important of the researchers in the theory of heat.^[7]

Later development

In 1876, physicist Willard Gibbs, building on the work of those as Clausius and Hermann von Helmholtz, situated the view that the measurement of "available energy" ΔG in a thermodynamic system could be mathematically accounted for by subtracting the "energy loss" TΔS from total energy change of the system ΔH. These concepts were further developed by James Clerk Maxwell [1871] and Max Planck [1903].

Entropy is said to be thermodynamically conjugate to temperature.

There is an important connection between entropy and the amount of internal energy in the system which is not available to perform work. In any process where the system gives up an energy ΔE, and its entropy falls by ΔS, a quantity at least T_R ΔS of that energy must be given up to the system's surroundings as unusable heat. Otherwise the process will not go forward. (T_R is the temperature of the system's external surroundings, which may not be the same as the system's current temperature T).

Classical thermodynamic views

Main article: classical thermodynamics

In 1803, mathematician Lazare Carnot, the father of Sadi Carnot, published a work entitled Fundamental Principles of Equilibrium and Movement. This work includes a discussion on the efficiency of fundamental machines, i.e. pulleys and inclined planes. Lazare Carnot saw through all the details of the mechanisms to develop a general discussion on the conservation of mechanical energy. Over the next three decades, Lazare Carnot’s theorem was taken as a statement that in any machine the accelerations and shocks of the moving parts all represent losses of moment of activity, i.e., of the useful work done. From this Lazare drew the inference that perpetual motion was impossible. This loss of moment of activity was the first-ever rudimentary statement of the second law of thermodynamics and the concept of 'transformation-energy' or entropy, i.e. energy lost to dissipation and friction.^[8]

In 1823, Lazare Carnot died in exile. The following year, in 1824, Lazare’s son Sadi Carnot having graduated from the Ecole Polytechnique training school for engineers, but now living on half-pay with his brother Hippolyte in a small apartment in Paris, wrote the Reflections on the Motive Power of Fire. In this paper, Sadi visualized an ideal engine in which the head of caloric converted into work could be reinstated by reversing the motion of the cycle, a concept subsequently known as thermodynamic reversibility. Sadi further postulated, however, that some caloric is lost, not being converted to mechanical work. Hence no real heat engine could realize the Carnot cycle's reversibility and was condemned to be less efficient. Hence, building on his father's work, Sadi positioned the concept that “some caloric is always lost”. This lost caloric was a precursory form of entropy loss as we now know it. Though formulated in terms of caloric, rather than entropy, this was an early insight into the second law of thermodynamics.

In the 1850s, Rudolf Clausius began to give this "lost caloric" a mathematical interpretation by questioning the nature of the inherent loss of heat when work is done, e.g. heat produced by friction.^[9]

Essentially, what Clausius did was to set forth the concept of the thermodynamic system and positioned the argument that in any irreversible process a small amount of heat energy dQ is incrementally dissipated across the system boundary. Specifically, in 1850 Clausius published his first memoir in which he presented a verbal argument as to why Carnot’s theorem, proposing the equivalence of heat and work, i.e. Q = W, was not perfectly correct and as such it would need amendment. In 1854, Clausius states: “In my memoir ‘On the Moving Force of Heat, &c.’, I have shown that the theorem of the equivalence of heat and work, and Carnot’s theorem, are not mutually exclusive, by that, by a small modification of the latter, which does not affect its principle, they can be brought into accordance.” This small modification on the latter is what developed into the second law of thermodynamics.

In his 1854 memoir, Clausius first develops the concepts of interior work, i.e. “those which the atoms of the body exert upon each other”, and exterior work, i.e. “those which arise from foreign influences which the body may be exposed”, which may act on a working body of fluid or gas, typically functioning to work a piston. He then discusses the three types of heat by which Q may be divided:

1. heat employed in increasing the heat actually existing in the body
2. heat employed in producing the interior work
3. heat employed in producing the exterior work

Building on this logic, and following a mathematical presentation of the first fundamental theorem, Clausius then presents us with the first-ever mathematical formulation of entropy, although at this point in the development of his theories calls it “equivalence-value”. He states, “the second fundamental theorem in the mechanical theory of heat may thus be enunciated:"^[10]

If two transformations which, without necessitating any other permanent change, can mutually replace one another, be called equivalent, then the generations of the quantity of heat Q of the temperature t from work, has the equivalence-value: and the passage of the quantity of heat Q from the temperature t1 to the temperature t2, has the equivalence-value: wherein T is a function of the temperature, independent of the nature of the process by which the transformation is effected.

This is the first-ever mathematical formulation of entropy; at this point, however, Clausius had not yet affixed the concept with the label entropy as we currently know it; this would come in the following two years.

In 1865, Clausius gave this heat loss a name:^[11]

In 1876, chemical engineer Willard Gibbs, building on the work of those as Clausius and Hermann von Helmholtz, situated the view that the measurement of “available energy” ΔG in a thermodynamic system could be mathematically accounted for by subtracting the “energy loss” TΔS from total energy change of the system ΔH. These concepts were further developed by James Clerk Maxwell [1871] and Max Planck [1903]. Carathéodory linked entropy with a mathematical definition of irreversiblity, in terms of trajectories and integrability.

Statistical thermodynamic views

Main article: statistical thermodynamics

In 1850, a mathematical formulation of entropy was first introduced in the context of classical thermodynamics by Rudolf Clausius in his analysis of Sadi Carnot's 1824 work on thermodynamic efficiency. It was not until 1865, however, that Clausius singled the quantity out and gave it the name “entropy” as derived from the Greek word en-trepein, meaning energy turned to waste.

In 1877, Ludwig Boltzmann formulated the alternative definition of entropy S defined as:

where

k_B is Boltzmann's constant and

Ω is the number of microstates consistent with the given macrostate.

Boltzmann saw entropy as a measure of statistical "mixedupness" or disorder. This concept was soon refined by J. Willard Gibbs, and is now regarded as one of the cornerstones of the theory of statistical mechanics.

Information theory views

Main article: information theory

An analog to thermodynamic entropy is information entropy. In 1948, while working at Bell Telephone Laboratories electrical engineer Claude Shannon set out to mathematically quantify the statistical nature of “lost information” in phone-line signals. To do this, Shannon developed the very general concept of information entropy, a fundamental cornerstone of information theory. Initially it seems that Shannon was not particularly aware of the close similarity between his new quantity and earlier work in thermodynamics. In 1949, however, when Shannon had been working on his equations for some time, he happened to visit the mathematician John von Neumann. Although the story varies, initially it seems that Shannon was not particularly aware of the close similarity between his new quantity and the earlier work in thermodynamics. During their discussions, regarding what Shannon should call the “measure of uncertainty” or attenuation in phone-line signals with reference to his new information theory, according to one source:^[12]

According to another source, when von Neumann asked him how he was getting on with his information theory, Shannon replied:^[13]

In 1948 Shannon published his famous paper “A Mathematical Theory of Communication”, in which he devoted a section to what he calls Choice, Uncertainty, and Entropy.^[14] In this section, Shannon introduces an “H function” of the following form:

where K is a positive constant. Shannon then states that “any quantity of this form, where K merely amounts to a choice of a unit of measurement, plays a central role in information theory as measures of information, choice, and uncertainty.” Then, as an example of how this expression applies in a number of different fields, he references R.C. Tolman’s 1938 Principles of Statistical Mechanics, stating that “the form of H will be recognized as that of entropy as defined in certain formulations of statistical mechanics where p_i is the probability of a system being in cell i of its phase space… H is then, for example, the H in Boltzmann’s famous H theorem.” As such, over the last fifty years, ever since this statement was made, people have been overlapping the two concepts or even stating that they are exactly the same.

Shannon's information entropy is a much more general concept than statistical thermodynamic entropy. Information entropy is present whenever there are unknown quantities that can be described only by a probability distribution. In a series of papers by E. T. Jaynes starting in 1957, the statistical thermodynamic entropy can be seen as just a particular application of Shannon's information entropy to the probabilities of particular microstates of a system occurring in order to produce a particular macrostate.

Popular use

The term entropy is often used in popular language to denote a variety of unrelated phenomena. One example is the concept of corporate entropy as put forward somewhat humorously by authors Tom DeMarco and Timothy Lister in their 1987 classic publication Peopleware, a book on growing and managing productive teams and successful software projects. Here, they view energy waste as red tape and business team inefficiency as a form of entropy, i.e. energy lost to waste. This concept has caught on and is now common jargon in business schools.

Terminology overlap

When necessary, to disambiguate between the statistical thermodynamic concept of entropy, and entropy-like formulae put forward by different researchers, the statistical thermodynamic entropy is most properly referred to as the Gibbs entropy. The terms Boltzmann-Gibbs entropy or BG entropy, and Boltzmann-Gibbs-Shannon entropy or BGS entropy are also seen in the literature.

See also

• Entropy
• Enthalpy
• Thermodynamic free energy

References