My watch list

Muon-catalyzed fusion

Muon-catalyzed fusion (μCF) is a process allowing nuclear fusion to take place at temperatures significantly lower than the temperatures required for thermonuclear fusion, even at room temperature or lower. Although it can be produced reliably with the right equipment and has been much studied, it is believed that the poor energy balance will prevent it from ever becoming a practical power source. However, if negatively charged muons (μ⁻) could be made more cheaply and efficiently somehow and/or if virtually every one made could somehow be used to catalyze as many nuclear fusion reactions as possible, the energy balance might improve enough for muon-catalyzed fusion to become a practical power source. It used to be known as cold fusion; however, this term is now avoided as it can create confusion with other suggested forms of room-temperature fusion that are rejected by mainstream science. A much more appropriate name would be cool fusion, particularly if muon-catalyzed fusion ever did become a practical power source.

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

What is the Sensitivity of my Balance?

Better weighing performance in 6 easy steps

1 Etymology
2 Deuterium-tritium (d-t or dt)
3 Deuterium-deuterium (d-d or dd) and other types
4 Process
5 A brief history
6 Some problems facing practical exploitation
7 Potential benefits
8 Some conclusions
9 Notes
10 References
11 See also

Etymology

This process is referred to as muon-catalyzed fusion because muons are crucial to the reaction mechanism, but are not themselves used up.

Deuterium-tritium (d-t or dt)

In the muon-catalyzed fusion of most interest, a positively charged deuteron (d), a positively charged triton (t), and a negatively charged muon essentially form a positively charged muonic molecular heavy hydrogen ion (d-μ-t)⁺.^[1] The muon is basically a heavy electron and, like an electron, is also a fundamental, point-like particle (as far as present day experimental measurements can tell).^[2] The muon has an electric charge identical to that of an electron, about -1.6x10^-19 coulomb.^[3]

The muon, with a rest mass about 207 times greater than the rest mass of an electron,^[4] is able to drag the more massive triton and deuteron about 207 times closer together to each other in the muonic (d-μ-t)⁺ molecular ion than can an electron in the corresponding positively charged electronic molecular hydrogen ion (d-e-t)⁺. The average separation between the triton and the deuteron in the electronic molecular ion is about one angstrom,^[5]^[6] so the average separation between the triton and the deuteron in the muonic molecular ion is about 207 times smaller than that.^[7]^[8]^[9] Due to the strong nuclear force, whenever the triton and the deuteron in the muonic molecular ion happen to get even closer to each other during their periodic vibrational motions, the probability is very greatly enhanced that the positively charged triton and the positively charged deuteron would undergo quantum tunnelling through the repulsive Coulomb barrier that acts to keep them apart.^[10] Indeed, the quantum mechanical tunnelling probability depends roughly exponentially on the average separation between the triton and the deuteron, allowing a single muon to catalyze the d-t nuclear fusion in less than about half a picosecond,^[11] once the muonic molecular ion is formed.^[5]

The formation time of the muonic molecular ion is one of the "rate-limiting steps" in muon-catalyzed fusion that can easily take up to ten thousand or more picoseconds in a liquid molecular deuterium and tritium mixture (D₂, DT, T₂), for example.^[5] Each catalyzing muon thus spends most of its ephemeral existence of about 2.2 microseconds,^[4]^[12] as measured in its rest frame wandering around looking for suitable deuterons and tritons with which to bind.

Another way of looking at muon-catalyzed fusion is to try to visualize the ground state orbit of a muon around either a deuteron or a triton.^[13] Suppose the muon happens to have fallen into an orbit around a deuteron initially, which it has about a 50% chance of doing if there are approximately equal numbers of deuterons and tritons present, forming an electrically neutral muonic deuterium atom (d-μ)⁰ that acts somewhat like a "fat, heavy neutron" due both to its relatively small size (again, about 207 times smaller than an electrically neutral electronic deuterium atom (d-e)⁰) and to the very effective "shielding" by the muon of the positive charge of the proton in the deuteron. Even so, the muon still has a much greater chance of being transferred to any triton that comes near enough to the muonic deuterium than it does of forming a muonic molecular ion. The electically neutral muonic tritium atom (t-μ)⁰ thus formed will act somewhat like an even "fatter, heavier neutron," but it will most likely hang on to its muon, eventually forming a muonic molecular ion, most likely due to the resonant formation of a hyperfine molecular state within an entire deuterium molecule D₂ (d=e²=d),^[14] with the muonic molecular ion acting as a "fatter, heavier nucleus" of the "fatter, heavier" neutral "muonic/electronic" deuterium molecule ([d-μ-t]=e²=d), as predicted by Vesman, an Estonian graduate student, in 1967.

Once the muonic molecular ion state is formed, the shielding by the muon of the positive charges of the proton of the triton and the proton of the deuteron from each other allows the triton and the deuteron to move close enough together to fuse with alacrity. The muon survives the d-t muon-catalyzed nuclear fusion reaction and remains available (usually) to catalyze further d-t muon-catalyzed nuclear fusions. Each exothermic d-t nuclear fusion releases about 17.6 MeV of energy in the form of a "very fast" neutron having a kinetic energy of about 14.1 MeV and an alpha particle α (a helium-4 nucleus) with a kinetic energy of about 3.5 MeV.^[5]^[15] An additional 4.8 MeV can be gleaned by having the fast neutrons moderated in a suitable "blanket" surrounding the reaction chamber, with the blanket containing lithium-6, whose nuclei, known by some as "lithions," readily and exothermically absorb thermal neutrons, the lithium-6 being transmuted thereby into an alpha particle and a triton.^[16]^[17]

Deuterium-deuterium (d-d or dd) and other types

The first kind of muon-catalyzed fusion to be observed experimentally, by L.W. Alvarez et al.,^[18] was actually protium (H or ₁H¹) and deuterium (D or ₁H²) muon-catalyzed fusion. The fusion rate for p-d (or pd) muon-catalyzed fusion has been estimated to be about a million times slower than the fusion rate for d-t muon-catalyzed fusion.^[5]^[19]

Of more practical interest, deuterium-deuterium muon-catalyzed fusion has been frequently observed and extensively studied experimentally, in large part because deuterium already exists in relative abundance and, like hydrogen, deuterium is not at all radioactive^[20]^[21] By way of contrast, tritium, with a half-life of about 12.5 years,^[4] must be painstakingly made atom by atom, most often in a nuclear fission reactor, using the lithion (lithium-6) thermal neutron absorption nuclear reaction described in the previous section. In addition, tritium is still radioactive enough to be inconvenient to work with, requiring both protective shielding and special handling.

The fusion rate for d-d muon-catalyzed fusion has been estimated to be only about 1% of the fusion rate for d-t muon-catalyzed fusion, but this still gives about one d-d nuclear fusion every 10 to 100 picoseconds^[22] or so.^[5] However, the energy released with every d-d muon-catalyzed fusion reaction is only about 20% or so of the energy released with every d-t muon-catalyzed fusion reaction.^[5] Moreover, the catalyzing muon has a probability of sticking to at least one of the d-d muon-catalyzed fusion reaction products that Jackson in this 1957 paper^[5] estimated to be at least 10 times greater than the corresponding probability of the catalyzing muon sticking to at least one of the d-t muon-catalyzed fusion reaction products, thereby preventing the muon from catalyzing any more nuclear fusions.^[23] Effectively, this means that each muon catalyzing d-d muon-catalyzed fusion reactions in pure deuterium is only able to catalyze about one-tenth of the number of d-t muon-catalyzed fusion reactions that each muon is able to catalyze in a mixture of equal amounts of deuterium and tritium, and each d-d fusion only yields about one-fifth of the yield of each d-t fusion, thereby making the prospects for useful energy release from d-d muon-catalyzed fusion at least 50 times worse than the already dim prosepects for useful energy release from d-t muon-catalyzed fusion.

Potential "aneutronic" (or substantially aneutronic) nuclear fusion possibilities, which result in essentially no neutrons among the nuclear fusion products, are almost certainly not very amenable to muon-catalyzed fusion.^[5] This is somewhat disappointing because aneutronic nuclear fusion reactions typically produce substantially only energetic charged particles whose energy could potentially be converted to more useful electrical energy with a much higher efficiency than is the case with the conversion of thermal energy. One such essentially aneutronic nuclear fusion reaction involves a deuteron from deuterium fusing with a helion (h⁺²) from helium-3, which yields an energetic alpha particle and a much more energetic proton, both positively charged (with a few neutrons coming from inevitable d-d nuclear fusion side reactions). However, one muon with only one negative electric charge is incapable of shielding both positive charges of a helion from the one positive charge of a deuteron. The chances of the requisite two muons being present simultaneously are exceptionally remote.

Process

To create this effect, a stream of negative muons, most often created by decaying pions, is sent to a block that may be made up of all three hydrogen isotopes (protium, deuterium, and/or tritium), where the block is usually frozen, and the block may be at temperatures of about 3 kelvin (-270 Celsius) or so. As said previously, the muon may bump the electron from one of the hydrogen isotopes. The muon, 207 times more massive than the electron, effectively shields and reduces the electromagnetic resistance between two nuclei and draws them much closer into a covalent bond than an electron can. Because the nuclei are so close, the strong nuclear force is able to kick in and bind both nuclei together. They fuse, release the catalytic muon (most of the time), and part of the original mass of both nuclei is released as energetic particles, as with any other type of nuclear fusion (see nuclear fusion to understand how this energy is released). The release of the catalytic muon is critical to continue the reactions. The majority of the muons continue to bond with other hydrogen isotopes and continue fusing nuclei together. However, there is a major drawback with muon-catalyzed fusion: not all of the muons are recycled, and too many bond with other debris emitted following the fusion of the nuclei (such as alpha particles and helions), removing the muons from the catalytic process. This gradually and ultimately chokes off the reactions, as there are fewer and fewer muons with which the nuclei may bond. The highest success rate achieved in the lab has been on the order of about 100 reactions or so per muon.

A brief history

Andrei Sakharov and F.C. Frank ^[24] predicted the phenomenon of muon-catalyzed fusion on theoretical grounds before 1950. Ya.B. Zel'dovitch^[25] also wrote about the phenomenon of muon-catalyzed fusion in 1954. As mentioned in the previous section, L.W. Alvarez et al.,^[18] when analyzing the outcome of some experiments with muons incident on a hydrogen bubble chamber at Berkeley in 1956, observed muon-catalysis of exothermic p-d, proton and deuteron, nuclear fusion, which results in a helion, a gamma ray, and a release of about 5.5 MeV of energy. The Alvarez experimental results, in particular, spurred the young John David Jackson^[26] to publish one of the first comprehensive theoretical studies of muon-catalyzed fusion in his ground-breaking 1957 paper.^[5] Jackson's 1957 paper^[5] also contained the first serious speculations on useful energy release from muon-catalyzed fusion. While not intending to spoil the "punchline," as Abraham Pais called it, since Jackson's 1957 paper^[5] is a delight to read and study, ^[27] Jackson regretfully concluded as far back as 1957 that useful energy or power production is unlikely, unless the "Gordian knot" of the so-called "alpha-sticking" problem (mentioned briefly above and discussed in somewhat more detail in the next section) could be unravelled and/or an energetically cheaper way of producing the catalyzing muons in the first place (also discussed more in the next section) could be found.^[5] So far, his not overly optimistic, yet fundamentally realistic, assessment has stood the test of time.

Some problems facing practical exploitation

One practical problem with the muon-catalyzed fusion process is that muons are unstable, decaying in about 2.2 microseconds (in their rest frame).^[4] Hence, there needs to be some cheap means of producing muons, and the muons must be arranged to catalyze as many nuclear fusion reactions as possible before decaying.

Another, and in many ways more serious, problem is the notorious "alpha-sticking" problem mentioned in the previous section, which was recognized by J.D. Jackson in his seminal 1957 paper.^[5]^[28] The α-sticking problem is the approximately 1% probability of the negatively charged muon "sticking" to the doubly positively charged alpha particle "ash" that results from the deuteron-triton nuclear fusion "burning," thereby effectively removing the muon from the muon-catalysis process altogether. Even if muons were absolutely stable, each muon could catalyze, on average, only about 100 d-t muon-catalyzed nuclear fusions before sticking to an alpha particle, which is only about one-fifth the number of d-t muon-catalyzed nuclear fusions needed to produce break-even, where more thermal energy is generated than the electrical energy that is consumed to produce the muons in the first place, according to Jackson's rough 1957 estimate.^[5]

More recent measurements seem to point to more encouraging values for the α-sticking probability, finding the α-sticking probability to be about 0.5% (or perhaps even about 0.4% or 0.3%), which could mean as many as about 200 (or perhaps even about 250 or about 333) muon-catalyzed d-t fusions per muon.^[29]^[30] Indeed, the team led by Steven E. Jones achieved 150 d-t fusions per muon (average) at the Los Alamos Meson Physics Facility.^[31] Unfortunately, 200 (or 250 or even 333) muon-catalyzed d-t fusions per muon are still not quite enough even to reach "break-even," where as much thermal energy is generated (or output) as the electrical energy that was used up (or input) to make the muon in the first place. This means, of course, that not nearly enough thermal energy is generated thereby to be able to convert the thermal energy released into more useful electrical energy, and to have any electrical energy left over to sell to the commercial electrical power "grid." The conversion efficiency from thermal energy to electrical energy is only about 40% or so. Also, some not inconsiderable fraction of that electrical energy (hopefully not all of it) would have to be "recycled" (used up in deuteron particle accelerators, for example) to make more muons to keep the muon-catalyzed d-t nuclear fusion fires burning night and day.^[32] The best recent estimated guess of the electrical "energy cost" per muon is about 6 GeV (billion electron Volts), using deuterons that are accelerated to have kinetic energies of about 800 MeV per nucleon, with accelerators that are (coincidentally) about 40% efficient at taking electrical energy from the Alternating Current (AC) mains (the plugs in the wall) and accelerating the deuterons using this electrical energy.

Potential benefits

If muon-catalyzed d-t nuclear fusion were able to be realized practically, it would be a much "greener" way of generating power than conventional nuclear fission reactors because muon-catalyzed d-t nuclear fusion (like most other types of nuclear fusion), produces far fewer harmful (and far less long-lived) radioactive wastes, and hardly any greenhouse gases. Practical and economically sensible muon-catalyzed d-t nuclear fusion would go a long way toward reducing the production of greenhouse gases, such as carbon dioxide (CO₂), by reducing or even eliminating the need to burn fossil fuels and biomass that contain carbon, for example.

Some people have proposed a "hybrid" fusion/nuclear fission schemes to use the large amount of neutrons produced in muon-catalyzed d-t nuclear fusions to "breed" fissile fuels, from "fertile" materials - for example, thorium-232 could breed uranium-233 in this way. The fissile fuels that have been bred can then be "burned," either in a conventional supercritical nuclear fission reactor or in an unconventional subcritical fission "pile." One example of an unconventional subcritical fission pile is an Accelerator-Driven System (ADS) that has been proposed for, and in some places is currently being developed for, the Accelerator Transmutation of Waste (ATW) - for example, using neutrons to transmute large quantities of highly radioactive and extremely long-lived nuclear wastes, such as those produced (mainly) by conventional nuclear fission reactors, into less harmful, less radioactive, less toxic, and much less long-lived transmuted elements. Another example of the creative use of an unconventional subcritical fission pile is the energy amplifier devised by Physics Nobel Laureate Carlo Rubbia, among others. ^[33] ^[34]

Some conclusions

Except for refinements such as these, not all that much has changed in nearly half a century since Jackson's assessment^[5] of the feasibility of muon-catalyzed fusion, other than Vesman's prediction of the hyperfine resonant formation of the muonic (d-μ-t)⁺ molecular ion, which was subsequently experimentally observed. This helped spark renewed interest in the whole field of muon-catalyzed fusion, which remains an active area of research worldwide among those who continue to be fascinated and intrigued (and frustrated) by this tantalizing approach to controllable nuclear fusion that almost works. Clearly, as Jackson observed in his 1957 paper, muon-catalyzed fusion is "unlikely" to provide "useful power production… unless an energetically cheaper way of producing μ⁻-mesons can be found."^[5]

Notes

^ The negatively charged muon is often simply called a muon, by analogy with the electron (e⁻), which is similarly negatively charged, but rarely if ever called a negative electron. A deuteron (d⁺ or, more commonly, d) is a positively charged deuterium nucleus, a single positively charged proton p⁺, or just p, bound by the strong nuclear force to a single electrically neutral neutron n⁰, or simply n. Deuterium is often also written as ₁H², using here the usual notation _ZH^A, where Z is the atomic number, the number of protons in the nucleus, and A is the atomic weight. Deuterium (D), like its more massive cousin, tritium (T), is one of the few isotopes to have its own capitalized element name. Deuterium is also known as "heavy" hydrogen (₁H¹ or simply H). Similarly, a triton (t⁺ or, traditionally, t) is a positively charged tritium nucleus, a single proton also bound by the strong nuclear force to two neutrons . Tritium (₁H³) should be known as "heavier" hydrogen, for the sake of consistency.
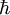^ The muon is also a fermion, having an intrinsic spin angular momentum equal in magnitude to one-half of Planck's constant, h, divided by 2π (where h divided by 2π is $\hbar$ , which is called "h-bar" and is also known as Dirac's constant), also identical to the intrinsic spin angular momentum of an electron.
^ The muon has an antiparticle, the positively charged muon (mu-bar⁺), sometimes called a "posimuon," again by analogy with the positron, e-bar⁺, predicted theoretically by Paul Adrian Maurice Dirac on the basis of his very own relativistic Dirac equation and then subsequently observed experimentally by Carl Anderson in his cosmic ray experiments, the positron being, of course, the antiparticle (antimatter counterpart) of the electron.
^ ^a ^b ^c ^d The values of the various physical constants and masses can be found at the National Institute of Standards and Technology website NIST Constants, for example.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q Jackson, J. D. (April 15, 1957). "Catalysis of Nuclear Reactions between hydrogen isotopes by μ⁻-Mesons". Physical Review 106: 330. doi:10.1103/PhysRev.106.330. (Note that, according to S. Cohen, D.L. Judd, and R.J. Riddell, Jr. in "μ-Mesonic Molecules. II. Molecular-Ion Formation and Nuclear Catalysis," Phys. Rev., 119, 397, July 1, 1960, footnote 16, Jackson may have been overly optimistic in Appendix D of his 1957 paper in his roughly calculated "guesstimate" of the rate of formation of a muonic (p-μ-p)⁺ molecular ion by a factor of about a million or so.)
^ One angstrom is defined to be a tenth of a nanometer or one ten-billionth of a meter, 10^-10 m.
^ In other words, the separation in the muonic case is about 500 femtometers (or million-billionths of a meter, 10^-15 m, also known as a fermi in honor of Enrico Fermi), which is about 354 times the Compton wavelength of a pion (h/(2π(m_πc))), which is very close to one femtometer times the square root of two (approximately 1.4x10^-15 m), where c is the speed of light in a vacuum, which is defined to be 299 792 458 meters per second, 2.99792458x10⁸ m/s or about 1.8 trillion furlongs per fortnight, and m_πc² is the rest mass energy of a pion, which is about 140 MeV. The pion's Compton wavelength is characteristic of the range of the strong nuclear force between nucleons (such as protons and neutrons) in atomic nuclei (at least the ones that are more complicated than a single proton, the nucleus of protium, otherwise known as hydrogen). The pion's Compton wavelength corresponds (roughly) to the effective "radius" of a typical atomic nucleus, when multiplied by the cube root of the atomic weight, A^1/3.
^ The strong nuclear force is (roughly) about a hundred times stronger in attracting a deuteron to a triton than the electromagnetic force is at repelling them, for example, at a distance between them on the order of the pion's Compton wavelength. The strong nuclear force is also sometimes understood to be analogous to a "color van der Waals force" between hadrons in the context of quantum chromodynamics, QCD. Hadrons may simply be defined to be any strongly interacting particles, including baryons, such as nucleons, and mesons, such as pions, kaons, and the like, all of which are understood to be composite states of various quarks, antiquarks, and gluons. Gluons are the quanta of QCD that mediate "chromic" interactions among quarks and antiquarks in much the same way that photons mediate electromagnetic interactions between electrically charged particles in the context of quantum electrodynamics (QED). Unlike photons, however, which do not themselves carry any electric charge, gluons are themselves involved in chromic interactions with each other, because they themselves carry color charges.
^ It should be noted that Greek language purists would most likely prefer gluons to be called "chromatons," derived from the genitive case χρωματος of the (third declension) neuter Greek word for color, χρωμα, in the same way that "photons" may have been derived from the genitive case φωτος of the (third declension) neuter Greek word for light, φως, but the ubiquitous usage of the word gluons may be hard to overcome.
^ The repulsive Coulomb barrier arises, of course, because like electric charges repel each other.
^ One picosecond is defined to be a trillionth of a second, 10^-12 s.
^ One microsecond (1 µs) is defined to be one millionth of a second, 10^-6 s.
^ The muon, if given a choice, would actually prefer to orbit a triton rather than a deuteron, since the triton is about half again as massive as the deuteron.
^ This somewhat clumsy notation attempts to convey the information that the neutral deuterium molecule has a covalent bond provided by the two electrons binding the two deuterons together.
^ An MeV is a million electron volts or about ten-trillionths of a joule, 1.6x10^-13 J.
^ Using the difference between the known rest masses of the n and ₃Li⁶ reactants, on the one hand, and the known rest masses of the α and t products, on the other, along with the conservation of momentum and the conservation of energy, the over-all energy release (the Q-value), as well as the respective non-relativistic or Galilean velocities and non-relativistic or Galilean kinetic energies of the α and t products may be readily calculated directly.
^ "Thermal neutrons" are neutrons that have been "moderated" by giving up most of their kinetic energy in collisions with the nuclei of the "moderating materials" or moderators, cooling down to "room temperature" and having a thermalized kinetic energy of about 0.025 eV, corresponding to an average "temperature" of about 300 kelvins or so.
^ ^a ^b L.W. Alvarez et al., Phys. Rev. 105, 1127 (1957).
^ In principle, of course, p-d nuclear fusion could be catalyzed by the electrons present in the odd HDO "heavy-ish" water molecule that naturally occurs at the level of about 1.5% of 1% in ordinary water (H₂O). However, because the proton and the deuteron would be more than 200 times farther apart in the case of the electronic HDO molecule than in the case of the muonic (p-μ-d)⁺ molecular ion, there has almost certainly never been even one p-d electron-catalyzed fusion (eCF) in all the vast wine-dark seas covering about three-quarters of the face of the Earth during all the long eons that water has existed here.
^ Except, of course, for the ever-so-slight chance of proton-decay predicted in most Grand Unified Theories (or GUTs).
^ Even though the amount of deuterium is only about 1.5% of 1% of the amount of hydrogen, since hydrogen is far and away the most abundant element in the Universe, there is more than enough deuterium in the seven seas to supply the energy and power needs of humankind at least several billion years (assuming humankind can figure out clever ways of making some kind of nuclear fusion work at all).
^ In other words, about 10 ps to 100 ps, 1x10^-11 s to 1x10^-10 s.
^ This "alpha-sticking" or "α-sticking" problem is mentioned briefly in the next section and then is discussed in more detail in the section after that.
^ F.C. Frank, Nature 160, 525 (1947).
^ Ya.B. Zel'dovitch, Doklady Akad. Nauk U.S.S.R. 95, 493 (1954).
^ This is the very same J.D. Jackson whose Classical Electrodynamics is well-known to, and well-loved by, physics graduate students everywhere.
^ Indeed, Jackson's 1957 paper could easily serve as the basis for a whole interdisciplinary course in atomic, molecular, and nuclear physics.
^ Jackson admirably gives due credit to Eugene P. Wigner for pointing the α-sticking problem out to him.
^ See, for example, "Cold Nuclear Fusion" by Johann Rafelski and Steven E. Jones in Scientific American, 257, 84 (1987).
^ Interestingly, very detailed and involved theoretical calculations of the α-sticking probability in muon-catalyzed d-t fusion appear to yield a higher value of about 0.69%, which is different enough from the experimental measurements that give 0.5% (or 0.4% or 0.3%) to be somewhat mysterious.
^ S.E. Jones, "Muon-Catalysed Fusion Revisited," Nature 321: 127-133 (1986).
^ One of the favorite and apparently preferred ways to make muons is to accelerate deuterons to have kinetic energies of about 800 MeV per nucleon (in the "lab frame," where the suitable target particles are essentially at rest) using one or more particle accelerators, popularly (although incorrectly) referred to as "atom-smashers" (really, they are more like "nuclei-smashers"), to smash the accelerated deuterons into an appropriate target, such as a gas of molecular deuterium and molecular tritium, for example. Useful particle accelerators could be linear accelerators (LINACs) or cyclotrons (with either superconducting or non-superconducting magnets). Smashing the deuterons having a kinetic energy of about 800 MeV per nucleon into other neutron-containing nuclei creates a fair number of negative pions (π^-'s), among other things. As long as these negative pions are kept away from positively charged nuclei that would strongly absorb the strongly-interacting negative pions, each negative pion will generally decay after about 26 nanoseconds (in its rest frame) into a muon and a muon antineutrino (ν_μ-bar).
^ The "breeding" takes place due to certain neutron-capture nuclear reactions, followed by beta-decays, the ejection of electrons and neutrinos from nuclei as neutrons within the nuclei decay into protons as a result of weak nuclear forces.
^ Technically, looking at beta-decay from the more fundamental quark perspective, a down quark present in a neutron, having one-third of the negative electric charge of an electron, decays into an up quark, having two-thirds of the positive electric charge of a positron, the antimatter counterpart of an electron, thereby changing the neutron, made up of two "valence" down quarks and one "valence" up quark, into a proton, made up of two "valence" up quarks and one "valence" down quark), due to "electro-weak" interactions, as explained, in part, by Physics Nobel Laureates Shelly Glashow, Abdus Salam, and Steve Weinberg, among others.

References

Alvarez et al., Phys. Rev. 105, 1127 (1957).
Cohen et al.,Phys. Rev., 119, 397 (1960).
Frank, Nature 160, 525 (1947).
Jackson, Phys. Rev., 106, 330, (1957).
National Institute of Standards and Technology NIST: The values of the various physical constants and masses can be found at the National Institute of Standards and Technology website NIST Constants, for example.
Rafelski and Jones in Scientific American, 257, 84 (1987).
Zel'dovitch, Doklady Akad. Nauk U.S.S.R. 95, 493 (1954).