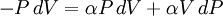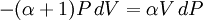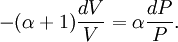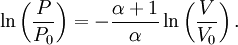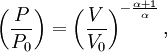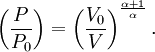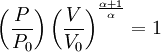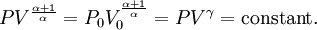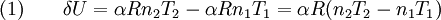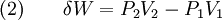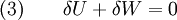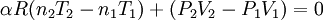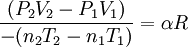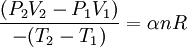To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Adiabatic process
In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which no heat is transferred to or from the working fluid. The term "adiabatic" literally means impassable (from Greek ἀ-διὰ-βαῖνειν, "ah-theeah-vainaein," not-through-to pass), corresponding here to an absence of heat transfer. For example, an adiabatic boundary is a boundary that is impermeable to heat transfer and the system is said to be adiabatically (or thermally) insulated; an insulated wall approximates an adiabatic boundary. Another example is the adiabatic flame temperature, which is the temperature that would be achieved by a flame in the absence of heat loss to the surroundings. An adiabatic process that is reversible is also called an isentropic process. The opposite extreme -- of maximum heat transfer with the surroundings, causing the temperature to remain constant -- is known as an isothermal process. Since temperature is thermodynamically conjugate to entropy, the isothermal process is conjugate to the adiabatic process for reversible transformations. A transformation of a thermodynamic system can be considered adiabatic when it is quick enough that no significant heat is transferred between the system and the outside. The adiabatic process can also be called quasi-static. At the opposite, a transformation of a thermodynamic system can be considered isothermal if it is slow enough so that the system's temperature remains constant by heat exchange with the outside. Additional recommended knowledge
Adiabatic heating and coolingAdiabatic heating and cooling are processes that commonly occur due to a change in the pressure of a gas. Adiabatic heating occurs when the pressure of a gas is increased. Diesel engines rely on adiabatic heating during their compression stroke to elevate the temperature sufficiently to ignite the fuel. Adiabatic heating also occurs in the Earth's atmosphere when an air mass descends, for example, in a katabatic wind or Foehn wind flowing downhill. Adiabatic cooling occurs when the pressure of a substance is decreased, such as when it expands into a larger volume. An example of this is when the air is released from a pneumatic tire; the outlet air will be noticeably cooler than the tire. Adiabatic cooling does not have to involve a fluid. One technique used to reach very low temperatures (thousandths and even millionths of a degree above absolute zero) is adiabatic demagnetisation, where the change in magnetic field on a magnetic material is used to provide adiabatic cooling. Adiabatic cooling also occurs in the Earth's atmosphere with orographic lifting and lee waves, and this can form pileus or lenticular clouds if the air is cooled below the dew point. Such temperature changes can be quantified using the ideal gas law, or the hydrostatic equation for atmospheric processes. It should be noted that no process is truly adiabatic. Many processes are close to adiabatic and can be easily approximated by using an adiabatic assumption, but there is always some heat loss. There is no such thing as a perfect insulator. Ideal gasThe mathematical equation for an ideal fluid undergoing an adiabatic process is where P is pressure, V is volume, and CP being the specific heat for constant pressure and CV being the specific heat for constant volume. α comes from the number of degrees of freedom divided by 2 (3/2 for monatomic gas, 5/2 for diatomic gas). For a monatomic ideal gas, γ = 5 / 3, and for a diatomic gas (such as nitrogen and oxygen, the main components of air) γ = 7 / 5. Note that the above formula is only applicable to classical ideal gases and not Bose-Einstein or Fermi gases. For adiabatic processes, it is also true that where T is an absolute temperature. This can also be written as Derivation of continuous formulaThe definition of an adiabatic process is that heat transfer to the system is zero, δQ = 0. Then, according to the first law of thermodynamics, where dU is the change in the internal energy of the system and δW is work done by the system. Any work (δW) done must be done at the expense of internal energy U, since no heat δQ is being supplied from the surroundings. Pressure-volume work δW done by the system is defined as However, P does not remain constant during an adiabatic process but instead changes along with V. It is desired to know how the values of dP and dV relate to each other as the adiabatic process proceeds. For an ideal gas the internal energy is given by where R is the universal gas constant and n is the number of moles in the system (a constant). Differentiating Equation (3) and use of the ideal gas law yields Equation (4) is often expressed as Now substitute equations (2), (3), and (4) into equation (1) to obtain simplify, divide both sides by PV, After integrating the left and right sides from Vo to V and from Po to P and changing the sides respectively, Exponentiate both sides, eliminate the negative sign, Therefore and Derivation of discrete formulaThe change in internal energy of a system, measured from state 1 to state 2, is equal to At the same time, the work done by the pressure-volume changes as a result from this process, is equal to Since we require the process to be adiabatic, the following equation needs to be true Substituting (1) and (2) in (3) leads to or If it's further assumed that there are no changes in molar quantity (as often in practical cases), the formula is simplified to this one: Graphing adiabatsAn adiabat is a curve of constant entropy on the P-V diagram. Properties of adiabats on a P-V diagram are:
The following diagram is a P-V diagram with a superposition of adiabats and isotherms:
The isotherms are the red curves and the adiabats are the black curves. The adiabats are isentropic. Volume is the abscissa (horizontal axis) and pressure is the ordinate (vertical axis). See also
Categories: Thermodynamic processes | Atmospheric thermodynamics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Adiabatic_process". A list of authors is available in Wikipedia. |





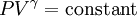
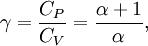
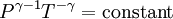
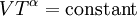
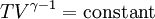
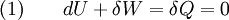
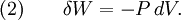
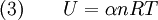
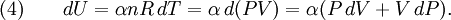
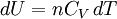 because
because