To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Temperature
Temperature is a physical property of a system that underlies the common notions of hot and cold; something that is hotter generally has the greater temperature. Temperature is one of the principal parameters of thermodynamics. On the microscopic scale, temperature is defined as simply the average energy of microscopic motions of a single particle in the system per degree of freedom. On the bulk scale, common to non-scientists, temperature is defined as that unique physical property that is shared between two otherwise entirely unlike things that happen to be in thermal equilibrium with each other (meaning, no net heat energy is exchanged between them). For a solid, these microscopic motions are principally the vibrations of the constituent atoms about their sites in the solid. For an ideal monatomic gas, the microscopic motions are the translational motions of the constituent gas particles. For multiatomic gas vibrational and rotational motion should be included too. Temperature is measured with thermometers that may be calibrated to a variety of temperature scales. In most of the world (except for the United States, Jamaica, and a few other countries), the Celsius scale is used for most temperature measuring purposes. The entire scientific world (the U.S. included) measures temperature using the Celsius scale and thermodynamic temperature using the kelvin scale, which is just the Celsius scale shifted downwards so that 0 K[1]= -273.15 °C, or absolute zero. Many engineering fields in the U.S., especially high-tech ones, also use the kelvin and Celsius scales. The bulk of the U.S. however, (its lay people, industry, popular meteorology, and government) relies upon the Fahrenheit scale. Other engineering fields in the U.S. also rely upon the Rankine scale (a shifted Fahrenheit scale) when working in thermodynamic-related disciplines such as combustion. Additional recommended knowledge
OverviewIntuitively, temperature is a measure of how hot or cold something is. On the molecular level, temperature is the result of the motion of particles which make up a substance. Temperature increases as the energy of this motion increases. The motion may be the translational motion of the particle, or the internal energy of the particle due to molecular vibration or the excitation of an electron energy level. Although very specialized laboratory equipment is required to directly detect the translational thermal motions, thermal collisions by atoms or molecules with small particles suspended in a fluid produces Brownian motion that can be seen with an ordinary microscope. The thermal motions of atoms are very fast and temperatures close to absolute zero are required to directly observe them. For instance, when scientists at the NIST achieved a record-setting cold temperature of 700 nK (1 nK = 10−9 K) in 1994, they used optical lattice laser equipment to adiabatically cool caesium atoms. They then turned off the entrapment lasers and directly measured atom velocities of 7 mm per second in order to calculate their temperature. Molecules, such as O2, have more degrees of freedom than single atoms: they can have rotational and vibrational motions as well as translational motion. An increase in temperature will cause the average translational energy to increase. It will also cause the energy associated with vibrational and rotational modes to increase. Thus a diatomic gas, with extra degrees of freedom like rotation and vibration, will require a higher energy input to change the temperature by a certain amount, i.e. it will have a higher heat capacity than a monatomic gas. The process of cooling involves removing energy from a system. When there is no more energy able to be removed, the system is said to be at absolute zero, which is the point on the thermodynamic (absolute) temperature scale where all kinetic motion in the particles comprising matter ceases and they are at complete rest in the “classic” (non-quantum mechanical) sense. By definition, absolute zero is a temperature of precisely 0 kelvins (−273.15 °C or −459.67 °F). Details
Contrary to other thermodynamic quantities such as entropy and heat, whose microscopic definitions are valid even far away from thermodynamic equilibrium, temperature being an average energy per particle can only be defined at thermodynamic equilibrium, or at least local thermodynamic equilibrium (see below). As a system receives heat, its temperature rises; similarly, a loss of heat from the system tends to decrease its temperature (at the--uncommon--exception of negative temperature; see below). When two systems are at the same temperature, no heat transfer occurs between them. When a temperature difference does exist, heat will tend to move from the higher-temperature system to the lower-temperature system, until they are at thermal equilibrium. This heat transfer may occur via conduction, convection or radiation or combinations of them (see heat for additional discussion of the various mechanisms of heat transfer) and some ions may vary . Temperature is also related to the amount of internal energy and enthalpy of a system: the higher the temperature of a system, the higher its internal energy and enthalpy. Temperature is an intensive property of a system, meaning that it does not depend on the system size, the amount or type of material in the system, the same as for the pressure and density. By contrast, mass, volume, and entropy are extensive properties, and depend on the amount of material in the system. The role of temperature in nature
Temperature plays an important role in almost all fields of science, including physics, chemistry, and biology. Many physical properties of materials including the phase (solid, liquid, gaseous or plasma), density, solubility, vapor pressure, and electrical conductivity depend on the temperature. Temperature also plays an important role in determining the rate and extent to which chemical reactions occur. This is one reason why the human body has several elaborate mechanisms for maintaining the temperature at 37 °C, since temperatures only a few degrees higher can result in harmful reactions with serious consequences. Temperature also controls the type and quantity of thermal radiation emitted from a surface. One application of this effect is the incandescent light bulb, in which a tungsten filament is electrically heated to a temperature at which significant quantities of visible light are emitted. Temperature-dependence of the speed of sound in air c, density of air ρ and acoustic impedance Z vs. temperature °C
Temperature measurementMain article: Temperature measurement, see also The International Temperature Scale. Temperature measurement using modern scientific thermometers and temperature scales goes back at least as far as the early 18th century, when Gabriel Fahrenheit adapted a thermometer (switching to mercury) and a scale both developed by Ole Christensen Rømer. Fahrenheit's scale is still in use, alongside the Celsius scale and the kelvin scale. Units of temperatureThe basic unit of temperature (symbol: T) in the International System of Units (SI) is the kelvin (Symbol: K). The kelvin and Celsius scales are, by international agreement, defined by two points: absolute zero, and the triple point of Vienna Standard Mean Ocean Water (water specially prepared with a specified blend of hydrogen and oxygen isotopes). Absolute zero is defined as being precisely 0 K and −273.15 °C. Absolute zero is where all kinetic motion in the particles comprising matter ceases and they are at complete rest in the “classic” (non-quantum mechanical) sense. At absolute zero, matter contains no thermal energy. Also, the triple point of water is defined as being precisely 273.16 K and 0.01 °C. This definition does three things: 1) it fixes the magnitude of the kelvin unit as being precisely 1 part in 273.16 parts the difference between absolute zero and the triple point of water; 2) it establishes that one kelvin has precisely the same magnitude as a one degree increment on the Celsius scale; and 3) it establishes the difference between the two scales’ null points as being precisely 273.15 kelvins (0 K = −273.15 °C and 273.16 K = 0.01 °C). Formulas for converting from these defining units of temperature to other scales can be found at Temperature conversion formulas. In the field of plasma physics, because of the high temperatures encountered and the electromagnetic nature of the phenomena involved, it is customary to express temperature in electronvolts (eV) or kiloelectronvolts (keV), where 1 eV = 11,604 K. In the study of QCD matter one routinely meets temperatures of the order of a few hundred MeV, equivalent to about 1012 K. For everyday applications, it's very often convenient to use the Celsius scale, in which 0 °C corresponds to the temperature at which water freezes and 100 °C corresponds to the boiling point of water at sea level. In this scale a temperature difference of 1 degree is the same as a 1 K temperature difference, so the scale is essentially the same as the kelvin scale, but offset by the temperature at which water freezes (273.15 K). Thus the following equation can be used to convert from degrees Celsius to kelvins. In the United States, the Fahrenheit scale is widely used. On this scale the freezing point of water corresponds to 32 °F and the boiling point to 212 °F. The following formula can be used to convert from Fahrenheit to Celsius: See temperature conversion formulas for conversions between most temperature scales. Negative temperatures
For some systems and specific definitions of temperature, it is possible to obtain a negative temperature. A system with a negative temperature is not colder than absolute zero, but rather it is, in a sense, hotter than infinite temperature.[2] Comparison of temperature scales
¹ The temperature scale is in disuse, and of mere historical interest.
Theoretical foundation of temperatureZeroth-law definition of temperatureWhile most people have a basic understanding of the concept of temperature, its formal definition is rather complicated. Before jumping to a formal definition, let us consider the concept of thermal equilibrium. If two systems with fixed volumes are brought together in thermal contact, changes most likely will take place in the properties of both systems. These changes are caused by the transfer of heat between the systems. A state must be reached in which no further changes occur, to put the objects into thermal equilibrium. A basis for the definition of temperature can be obtained from the so-called zeroth law of thermodynamics which states that if two systems, A and B, are in thermal equilibrium and a third system C is in thermal equilibrium with system A then systems B and C will also be in thermal equilibrium (being in thermal equilibrium is a transitive relation; moreover, it is an equivalence relation). This is an empirical fact, based on observation rather than theory. Since A, B, and C are all in thermal equilibrium, it is reasonable to say each of these systems shares a common value of some property. We call this property temperature. Generally, it is not convenient to place any two arbitrary systems in thermal contact to see if they are in thermal equilibrium and thus have the same temperature. Also, it would only provide an ordinal scale. Therefore, it is useful to establish a temperature scale based on the properties of some reference system. Then, a measuring device can be calibrated based on the properties of the reference system and used to measure the temperature of other systems. One such reference system is a fixed quantity of gas. The ideal gas law indicates that the product of the pressure and volume (P · V) of a gas is directly proportional to the temperature:
where 'T is temperature, n is the number of moles of gas and R is the gas constant. Thus, one can define a scale for temperature based on the corresponding pressure and volume of the gas: the temperature in kelvins is the pressure in pascals of one mole of gas in a container of one cubic metre, divided by 8.31... In practice, such a gas thermometer is not very convenient, but other measuring instruments can be calibrated to this scale. It is also interesting to note that pressure, volume, and the number of moles of a substance are all inherently greater than or equal to zero. This suggests that temperature must also be greater than or equal to zero. As a practical matter it is not possible to use a gas thermometer to measure absolute zero temperature since the gasses tend to condense into a liquid long before the temperature reaches zero. It is possible, however, to extrapolate how many degrees below the present temperature the absolute zero is from the temperature range where Equation 1 works. Temperature in gasesFor an ideal gas the kinetic theory of gases uses statistical mechanics to relate the temperature to the average kinetic energy of the atoms in the system. This average energy is independent of particle mass, which seems counter-intuitive to many people. Temperature is related only to the average kinetic energy of the particles in a gas - each particle has its own energy which may or may not correspond to the average; the distribution of energies (and thus speeds) of the particles in any gas are given by the Maxwell-Boltzmann distribution.
The temperature of an ideal gas is related to its average kinetic energy via the equation:
In the case of a monoatomic gas, the kinetic energy is: (Note that a calculation of the kinetic energy of a more complicated object, such as a molecule, is slightly more involved. Additional degrees of freedom are available, so molecular rotation or vibration must be included.) Temperature of the vacuumIt is possible to use the zeroth law definition of temperature to assign a temperature to something we don't normally associate temperatures with, like a perfect vacuum. Because all objects emit black body radiation, a thermometer in a vacuum away from thermally radiating sources will radiate away its own thermal energy; decreasing in temperature indefinitely until it reaches the zero-point energy limit. At that point it can be said to be in equilibrium with the vacuum and by definition at the same temperature. If we could find a gas that behaved ideally all the way down to absolute zero the kinetic theory of gases tells us that it would achieve zero kinetic energy per particle, and thereby achieve absolute zero temperature. Thus, by the zeroth law a perfect, isolated vacuum is at absolute zero temperature. Note that in order to behave ideally in this context it is necessary for the atoms of the gas to have no zero point energy. It will turn out not to matter that this is not possible because the second law definition of temperature will yield the same result for any unique vacuum state. More realistically, no such ideal vacuum exists. For instance a thermometer in a vacuum chamber which is maintained at some finite temperature (say, chamber is in the lab at room temperature) will equilibrate with the thermal radiation it receives from the chamber and with time reaches the temperature of the chamber. If a thermometer orbiting the Earth is exposed to a sunlight, then it equilibrates at the temperature at which power received by the thermometer from the Sun is exactly equal to the power radiated away by thermal radiation of the thermometer. For a black body this equilibrium temperature is about 281 K (+8 °C). Earth average temperature (which is maintained by similar balance) is close to this temperature. A thermometer isolated from solar radiation (in the shade of the Earth, for example) is still exposed to thermal radiation of Earth - thus will show some equilibrium temperature at which it receives and radiates equal amount of energy. If this thermometer is close to Earth then its equilibrium temperature is about 236 K (-37 °C) provided that Earth surface is at 281 K. A thermometer far away from Solar system still receives Cosmic microwave background radiation. Equilibrium temperature of such thermometer is about 2.725 K, which is the temperature of a photon gas constituting black body microwave background radiation at present state of expansion of Universe. This temperature is sometimes referred to as the temperature of space. Second-law definition of temperatureIn the previous section temperature was defined in terms of the Zeroth Law of thermodynamics. It is also possible to define temperature in terms of the second law of thermodynamics, which deals with entropy. Entropy is a measure of the disorder in a system. The second law states that any process will result in either no change or a net increase in the entropy of the universe. This can be understood in terms of probability. Consider a series of coin tosses. A perfectly ordered system would be one in which either every toss comes up heads or every toss comes up tails. This means that for a perfectly ordered set of coin tosses, there is only one set of toss outcomes possible: the set in which 100% of tosses came up the same. On the other hand, there are multiple combinations that can result in disordered or mixed systems, where some fraction are heads and the rest tails. A disordered system can be 90% heads and 10% tails, or it could be 40% heads and 60% tails, et cetera. As the number of coin tosses increases, the number of possible combinations corresponding to imperfectly ordered systems increases. For a very large number of coin tosses, the number of combinations corresponding to ~50% heads and ~50% tails dominates and obtaining an outcome significantly different from 50/50 becomes extremely unlikely. Thus the system naturally progresses to a state of maximum disorder or entropy. We previously stated that temperature controls the flow of heat between two systems and we have just shown that the universe, and we would expect any natural system, tends to progress so as to maximize entropy. Thus, we would expect there to be some relationship between temperature and entropy. In order to find this relationship let's first consider the relationship between heat, work and temperature. A heat engine is a device for converting heat into mechanical work and analysis of the Carnot heat engine provides the necessary relationships we seek. The work from a heat engine corresponds to the difference between the heat put into the system at the high temperature, qH and the heat ejected at the low temperature, qC. The efficiency is the work divided by the heat put into the system or:
where wcy is the work done per cycle. We see that the efficiency depends only on qC/qH. Because qC and qH correspond to heat transfer at the temperatures TC and TH, respectively, qC/qH should be some function of these temperatures:
Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, a heat engine operating between T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and T2, and the second between T2 and T3. This can only be the case if: which implies:
Since the first function is independent of T2, this temperature must cancel on the right side, meaning f(T1,T3) is of the form g(T1)/g(T3) (i.e. f(T1,T3) = f(T1,T2)f(T2,T3) = g(T1)/g(T2)· g(T2)/g(T3) = g(T1)/g(T3)), where g is a function of a single temperature. We can now choose a temperature scale with the property that:
Substituting Equation 4 back into Equation 2 gives a relationship for the efficiency in terms of temperature:
Notice that for TC = 0 K the efficiency is 100% and that efficiency becomes greater than 100% below 0 K. Since an efficiency greater than 100% violates the first law of thermodynamics, this implies that 0 K is the minimum possible temperature. In fact the lowest temperature ever obtained in a macroscopic system was 20 nK, which was achieved in 1995 at NIST. Subtracting the right hand side of Equation 5 from the middle portion and rearranging gives: where the negative sign indicates heat ejected from the system. This relationship suggests the existence of a state function, S, defined by:
where the subscript indicates a reversible process. The change of this state function around any cycle is zero, as is necessary for any state function. This function corresponds to the entropy of the system, which we described previously. We can rearranging Equation 6 to get a new definition for temperature in terms of entropy and heat:
For a system, where entropy S may be a function S(E) of its energy E, the temperature T is given by:
ie. the reciprocal of the temperature is the rate of increase of entropy with respect to energy. See also
References
Categories: Temperature | Heat | Thermodynamics | Atmospheric thermodynamics |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Temperature". A list of authors is available in Wikipedia. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- Dow and Davy License LP OxoSM Technology in Shandong, P.R. China
- Germany’s hydrogen strategy: More consistent focus on green hydrogen needed - Now is the time to establish viable hydrogen supply chains
- ALTANA Acquires Production of Metalure Pigments from Avery Dennison
- Solvay signs agreement to sell Caprolactones business to Perstorp
- Enzon Announces Resignation of Chief Financial Officer





![\mathrm{K = [^\circ C] \left(\frac{1 \, K}{1\, ^\circ C}\right) + 273.15\, K}](images/math/9/9/1/9912b6ce5daa2c92bc3d79557c739e43.png)
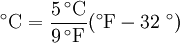
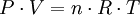 (1)
(1)
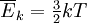 , where
, where 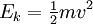
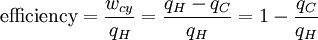 (2)
(2)
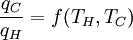 (3)
(3)
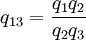
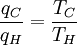 (4)
(4)
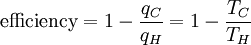 (5)
(5)
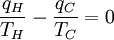
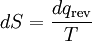 (6)
(6)
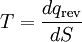 (7)
(7)
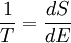 (8)
(8)


